Motivation¶

- the SCIP Optimization Suite is a powerful
mathematical optimization toolbox (LP, CIP, MINLP, ...) - acclaimed in academia and industry
- available in source code
- writing C/C++ code can be tough and time consuming
Python as a practical solution¶
- fast protoyping of new algorithmic ideas
- vast number of readily available Python libraries
- no need to compile your code
- easy and intuitive modeling (also with non-linear expressions)
- ...
Simple modeling example¶
$ \begin{alignat*}{27} \mbox{minimize }\; & x + y \\ \mbox{subject to }\; & 2x + y^2 &\;\geq\;& 10\\ & x, y &\;\geq\; & 0\\ & x \in \mathbb{R}, && y \in \mathbb{Z} \end{alignat*} $
... with PySCIPOpt:¶
In [2]:
from pyscipopt import Model
model = Model()
x = model.addVar('x')
y = model.addVar('y', vtype='I')
model.addCons(2*x + y*y >= 10)
model.setObjective(x+y)
model.optimize()
print('x: ', model.getVal(x), ', y: ', model.getVal(y), ', obj: ', model.getObjVal())
x: 0.5 , y: 3.0 , obj: 3.5
Some details about PySCIPOpt¶
- based on Cython
- requires headers and a library of the SCIP Optimization Suite
- organized in two main files
scip.pyxandscip.pxdand files for every supported plug-in:pricer.pxiheuristic.pxi- ...
- allows for straight-forward extensions
- hides complexity by setting many default parameters
- documented using docstring conventions
What is a callback?¶
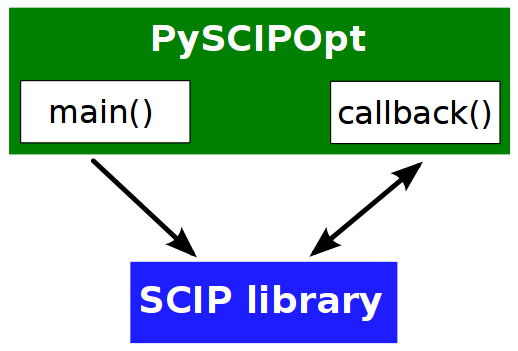 |
|
Example of a plug-in: TSP Constraint Handler¶
- SCIP only sees simple Travelling Salesman relaxation
- no subtour elimination constraints
- only connectivity of nodes is required
- subtour elimination by adding cuts
- optimal if no more subtours are present
> iterative process that calls Python code multiple times
In [8]:
import networkx
from pyscipopt import Model, Conshdlr, SCIP_RESULT
class TSPconshdlr(Conshdlr):
def __init__(self, variables):
self.variables = variables
- define method to find subtours in current solution:
In [9]:
def find_subtours(self, solution=None):
edges = []
x = self.variables
for (i,j) in x:
if self.model.getSolVal(solution, x[i,j]) > 1e-6:
edges.append((i,j))
G = networkx.Graph()
G.add_edges_from(edges)
components = list(networkx.connected_components(G))
return [] if len(components) == 1 else components
- implement
TSPconshdlrcallback for feasibility checking
In [10]:
def conscheck(self, constraints, solution, check_integrality,
check_lp_rows, print_reason):
if self.find_subtours(solution):
return {"result": SCIP_RESULT.INFEASIBLE}
else:
return {"result": SCIP_RESULT.FEASIBLE}
- implement
TSPconshdlrcallback for LP enforcement
In [11]:
def consenfolp(self, constraints, n_useful_conss, sol_infeasible):
subtours = self.find_subtours()
if subtours:
x = self.variables
for subset in subtours:
self.model.addCons(quicksum(x[i,j] for(i,j) in pairs(subset))
<= len(subset) - 1)
print("cut: len(%s) <= %s" % (subset, len(subset) - 1))
return {"result": SCIP_RESULT.CONSADDED}
else:
return {"result": SCIP_RESULT.FEASIBLE}
In [16]:
conshdlr = TSPconshdlr(x) # x = variables
model.includeConshdlr(conshdlr, "TSP", "TSP subtour eliminator",
needscons=False)
model.optimize()
Outlook¶
- further extend functionality, e.g. cover more SCIP functions
- support more plug-in types, e.g. node selector, presolver
implement support for general non-linear constraints
... but most importantly:
Get involved!¶
PySCIPOpt is hosted on GitHub:
http://github.com/SCIP-Interfaces/PySCIPOpt
Install with conda or as
python setup.py install
- Send us your pull requests!
- Open feature requests and report issues!
- Access the latest and greatest (no fixed release cycle)!
