Recent highlights
Confinement and driving cause memory for overdamped motion
Background & motivation: The transport of individual particles in inhomogeneous environments, shaped by geometric constraints or confining potentials, is inherently complex and often exhibits non-Markovian behavior. where states depend solely on the present, non-Markovian systems rely on the system's history, indicating the presence of memory. This memory can be quantified using a memory function within the framework of the generalized Langevin equation (GLE). A relatively simple example of motion leading to memory effects is particle behavior in a periodic potential energy landscape. A particularly challenging and intriguing question is how to adapt the GLE formalism to nonequilibrium conditions. Additionally, while the conventional GLE formalism typically addresses underdamped systems, a significant class of systems exhibits strongly overdamped motion, requiring appropriate modifications of the GLE.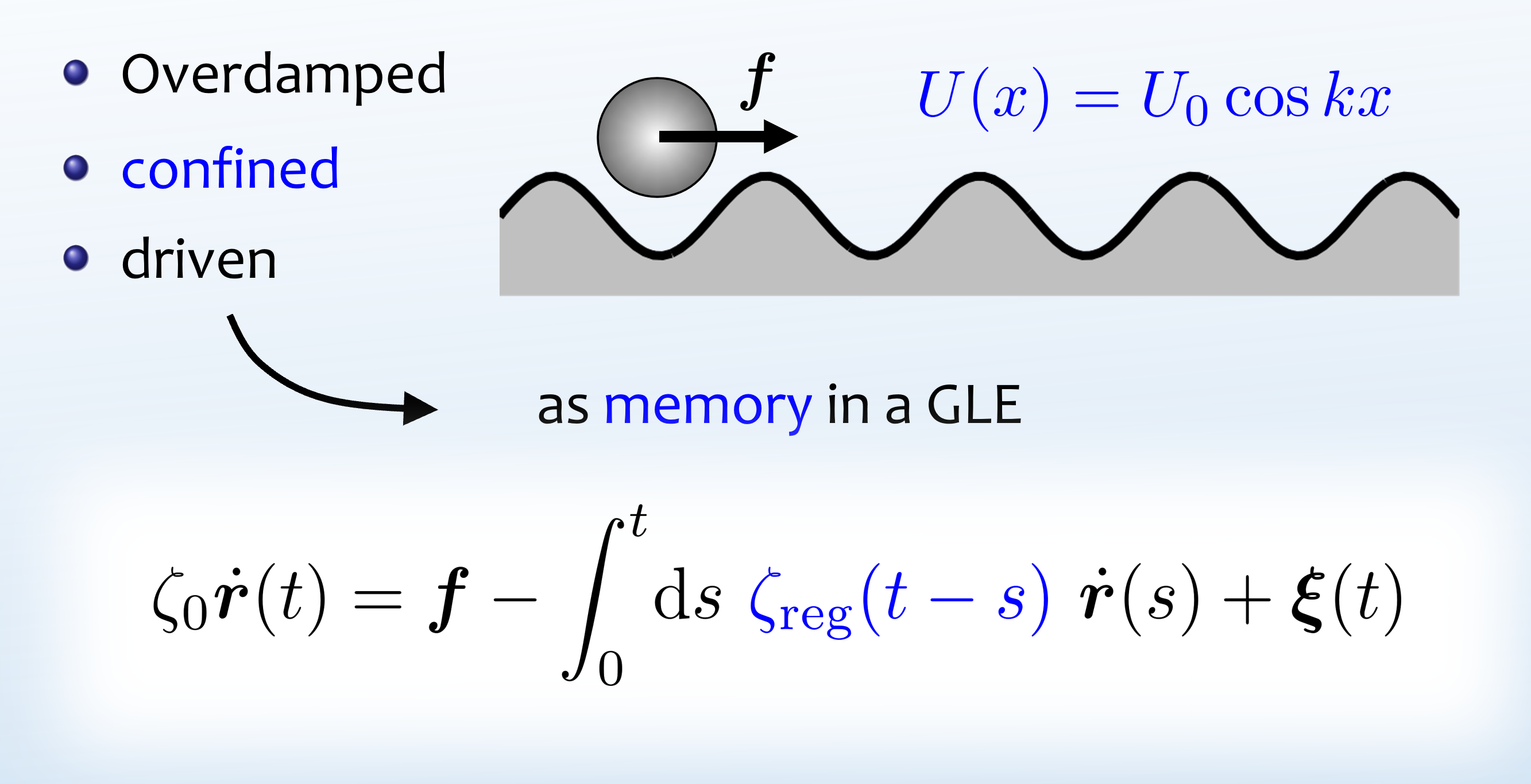
Figure: The overdamped motion of a particle driven over a sinusoidal potential energy landscape. The complexity of motion can be encapsulated in the memory function within the framework of the overdamped (linear) generalized Langevin equation.
Findings: We examine the impact of steady driving on the memory function of a colloidal system undergoing one-dimensional Brownian motion in a sinusoidal potential. To obtain the overdamped limit of the generalized Langevin equation (GLE), we separate the memory function into a singular (Markovian) and a regular (non-Markovian) part. Using exact solutions, we show that the random force in the GLE develops a bias under nonequilibrium conditions, supporting a recent theoretical prediction. From Brownian dynamics simulations, we estimate the memory function for different driving strengths based on mean-square displacement (MSD) data. Our results indicate that even moderate driving accelerates the decay of the memory function by several orders of magnitude. Notably, memory can persist on much longer timescales than expected from the convergence of the MSD to its long-time asymptote. Furthermore, the memory function shifts from a monotonic decay to a damped oscillatory behavior due to the interplay between confined motion and depinning. Our analysis also reveals significant non-Gaussianity, which challenges the Gaussian approximation of the random force in the GLE.
Publication:
A.V. Straube, F. Höfling,
Memory effects in colloidal motion under confinement and driving,
J. Phys. A: Math. Theor. 57, 295003 (2024) (open access)
