According to the German Clean Road Vehicle Procurement Act, in force since 2021, 45% of newly purchased public transport vehicles must be powered by alternative fuels, and 65% from 2026. In line with this legal requirement, many local transport companies are currently converting their bus fleets to battery-powered electric drive systems. Large cities such as Berlin, Hamburg, and Munich are working to fully electrify their bus fleets by 2030.
Electric buses (e-buses) are still more expensive than their counterparts with combustion engines and their purchase requires investments in specialized charging infrastructure, which for cost reasons is being built preferably in the form of slow chargers in bus depots and additionally as fast chargers at selected terminals. The comparatively shorter range of electric buses, especially in winter and summer, when heating and air conditioning consume significant amounts of additional energy, often requires charging en route. Charging times and detours that may occur hence need to be planned. It is also crucial to bear in mind that energy prices can fluctuate widely during the day and that the capacity of the local electricity grid may be subject to dynamic constraints, which is particularly important for night-time depot charging of the entire fleet. Load peaks due to simultaneous charging should be prevented as far as possible. It is therefore imperative not only to optimize vehicle deployment through vehicle rotations, but also to carefully select the charging events, which requires integrated bus circulation and charging planning (see Figure 1).
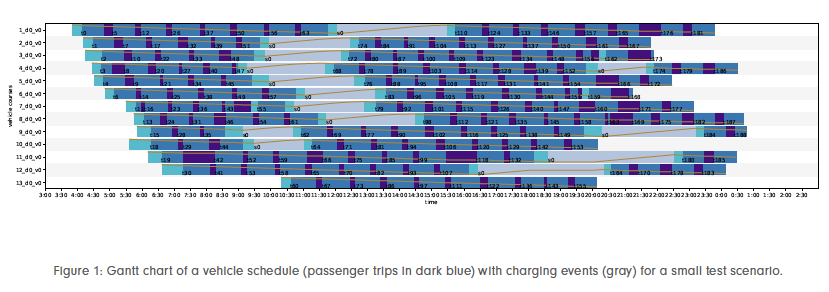
We developed a novel method at the Zuse Institute Berlin in the MobilityLab of the MODAL research campus together with our industry partner IVU Traffic Technologies AG. The algorithm enables the calculation of cost-minimal bus schedules with integrated optimization of the battery’s state of charge (SoC), while complying with capacity conditions at individual and combined charging points. The treatment of mixed e-bus and diesel fleets, which is important in a transition phase, is also possible.
Bus batteries are charged like conventional batteries using the so-called CC-CV (Constant Current - Constant Voltage) scheme. The SoC increases almost linearly up to about 80% under a constant charging rate, while for the last 20% the maximum permissible charging power then decreases rapidly. However, this last fifth of the battery capacity is important in order to make the best possible use of the performance of expensive electric buses. This charging process is generally modeled in terms of a so-called charge curve ζ, where ζ(?) gives the final SoC of an initially empty battery that has been charged for a period of time (?). Pre-existing planning methods are based on a linear or piecewise linear approximation of this function. One of the main innovations of our approach is the insight that this approach turns out to be inadequate for two reasons.
On the one hand, the aforementioned conditions result in local transport operators implementing an active charging management, which dynamically throttles the charging power depending on the current electricity price and the grid load. It can therefore not be assumed that charging is always carried out at maximum power, but that the selection of the charging curve itself is a variable. But instead of one charging curve, then all possible charging curves would have to be taken into account.
On the other hand, it is – at first sight paradoxically – possible that an underestimating approximation of the charging curve results in an overestimation of the state of charge, as shown in Figure 2.
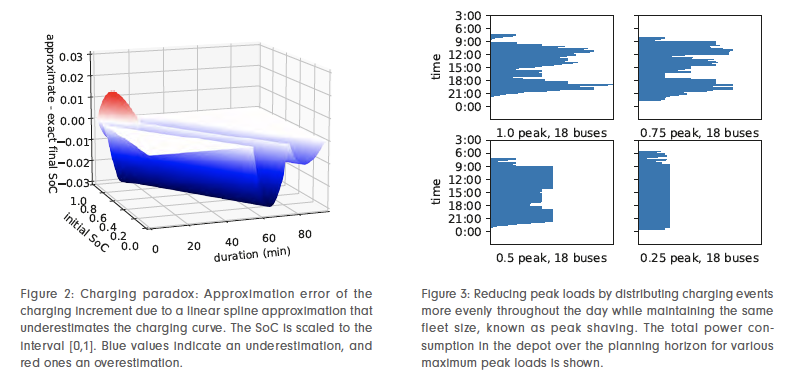
Indeed, batteries usually have an initial residual state of charge ? and we are interested in the charge increment ∆ζ(?,?)=ζ(ζ-1(?)+?)-?, which indicates how much the charging event increases the SoC. But this function depends mainly on the charging rate, which can be overestimated by piecewise linear approximations of the charging curve. Instead of the charging curve, we approximate the charge increment function with a piecewise linear underestimation and are able to show that the SoC is never overestimated. In addition, approximations involving only three sections with time increments of five minutes already lead to demonstrably negligible errors in the per mille range.
Our charging model also makes it easier to take into account electricity costs and grid capacities that depend on the time of day. In all cases we considered, it was possible to reduce the peak grid load of an unrestricted reference scenario by 50% to 75% without incurring an additional vehicle demand by optimizing the cycles and the charging in an integrated manner; see Figure 3 for an example.
