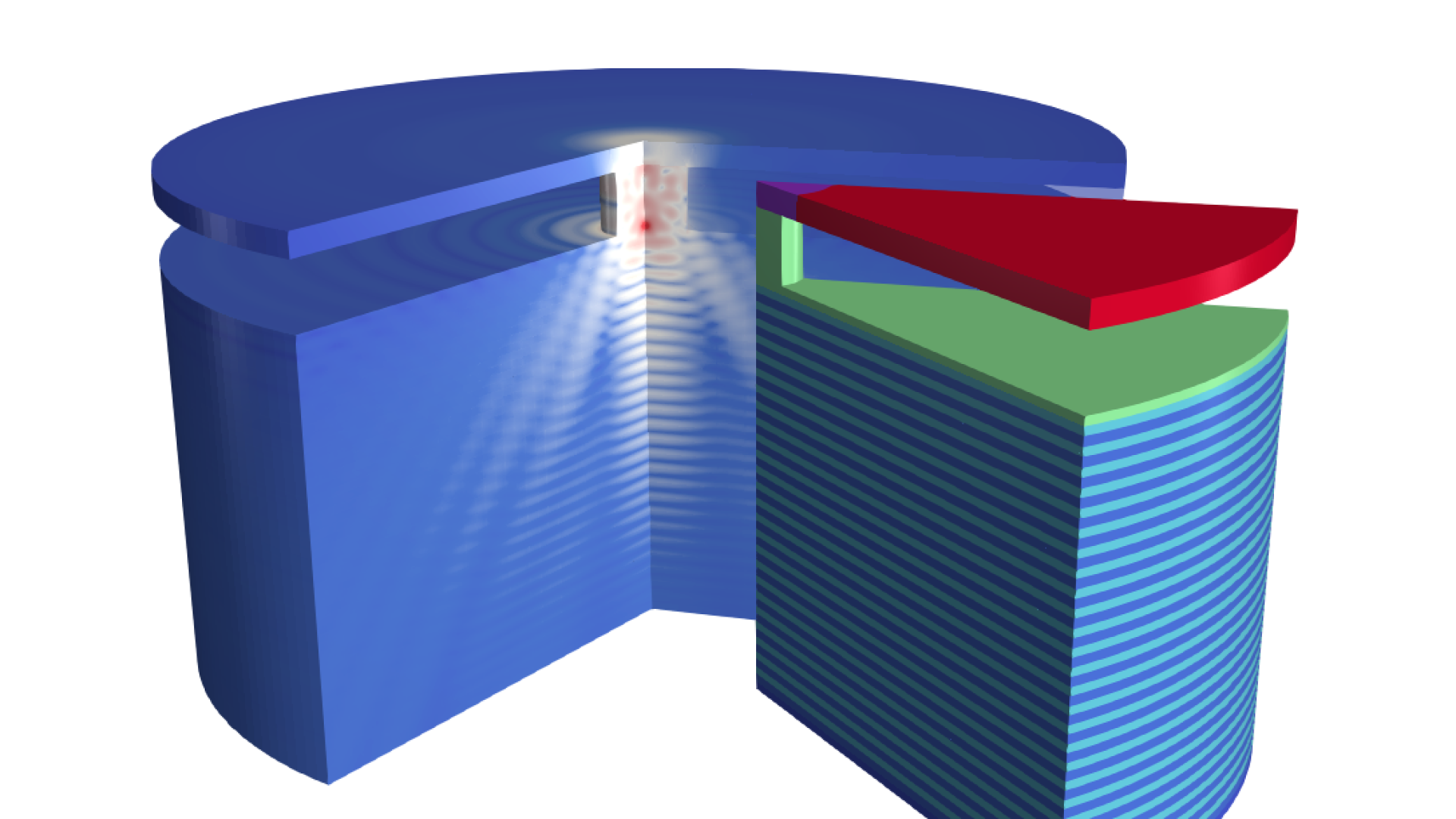
For centuries, classical physics has been the foun-dation for our understanding of the world around us. This still is true for large-scale phenomena, including our everyday perception of the world, and most engineering problems. However, for about 100 years now there exists another theory for describing nature on the atomic and sub-atomic scales. This theory is called quantum mechanics and it introduces rules vastly differ-ing from our classical intuitions. Phenomena pre-dicted by quantum mechanics can seem para-doxical and have surprised scientists ever since. One famous example of this is entanglement: the properties of two microscopic particles can-not be described independently of each other, even when they are very far apart and cannot exchange information. The setting of this exam-ple can be paraphrased as a game in which two players are being simultaneously asked ques-tions in separate rooms. By leveraging quantum entanglement, they can establish a link between their answers that cannot be explained by classi-cal physics. The experimental demonstration of this groundbreaking concept, proposed by physi-cist John Bell in the 1960s [1], earned the Nobel Prize in Physics in 2022. In a recently published work, researchers at ZIB were able to provide better theoretical bounds, which characterize when this effect can occur [3].
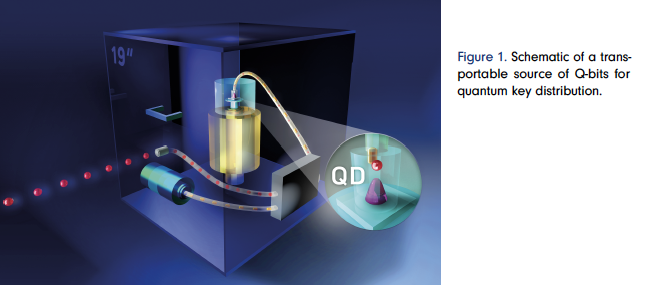
Historically, quantum mechanics has been indispensable in advancing technology, facilitat-ing the creation of groundbreaking devices like transistors, lasers, and atomic clocks. Accord-ingly, another area of focus is on engineering quantum sources that emit single photons, the basic units of light. These devices have potential applications in secure quantum communication, where interception is impossible. Together with external partners, researchers at ZIB were able to realize transportable quantum light sources with record-breaking photon generation rates, close to commercialization in quantum cryptog-raphy systems [4], and other building blocks for integrated quantum photonics [2, 7, 9, 10]. These devices can further be used as building blocks for the development of quantum comput-ers, which are expected to be able to drastically outperform classical computers in certain compu-tational tasks. Despite much effort, creating new quantum algorithms is still extremely challeng-ing. At ZIB, researchers are exploring various methods to develop new quantum algorithms and to improve existing ones. One promising area of active research involves running dynam-ical systems on quantum computers [6, 8]. This is of great interest for studying various physical phenomena, such as many particle systems in different energy environments.
Unfortunately, quantum computers are still in the developmental phase, struggling with hard-ware scalability limitations and other persistent obstacles. Interestingly however, classical com-puters can simulate quantum algorithms, offer-ing a pathway to a deeper understanding of quantum processes. This often leads to the gen-eration of vast amounts of data, which are too big to be processed. To tackle this challenge, researchers at ZIB are developing techniques to decompose large data structures into smaller components, helping classical computers to use their resources more efficiently for faster and improved simulations of quantum algorithms [5]. By collaborating with international research institutes and combining expertise from diverse fields such as mathematics, computer science, and physics, we aim to push the boundaries of quantum algorithm development and pioneer revolutionary applications in computation, com-munication, and beyond.
References:
[1] J. S. Bell. On the Einstein Podolsky Rosen paradox. Physics 1.3 (1964), 195–200. DOI: 10.1103/PhysicsPhysiqueFizika.1.195.
[2] R. Colom, F. Binkowski, F. Betz, Y. Kivshar, and S. Burger. Enhanced purcell factor for nanoantennas supporting interfering resonances. Phys. Rev. Research 4 (2022), 023189. DOI: 10.1103/PhysRevResearch.4. 023189.
[3] S. Designolle, G. Iommazzo, M. Besan çon, S. Knebel, P. Gelß, and S. Pokutta. Improved local models and new Bell inequalities via Frank-Wolfe algorithms. Phys. Rev. Res. 5 (4 2023), 043059. DOI: 10.1103/PhysRevResearch.5.043059.
[4] T. Gao, L. Rickert, F. Urban, J. Große, N. Srocka, S. Rodt, A. Musial, K. Zolnacz, P. Mergo, K. Dybka, W. Urbanczyk, G. Sek, S. Burger, S. Reitzenstein, and T. Heindel. A quantum key distribution testbed using a plug&play telecom-wavelength single-photon source. Appl. Phys. Rev. 9 (2022), 011412. DOI 10.1063/5.0070966.
[5] P. Gelß, R. Klein, S. Matera, and B. Schmidt. Solving the time-independent Schrödinger equation for chains of coupled excitons and phonons using tensor trains. The Journal of Chemical Physics 156.2 (2022), 024109. DOI: 10.1063/5.0074948. URL: https://doi.org/ 10.1063/5.0074948.
[6] J. Riedel, P. Gelß, R. Klein, and B. Schmidt. WaveTrain: A Python package for numerical quantum mechanics of chain-like systems based on tensor trains. The Journal of Chemical Physics 158.16 (2023), 164801. DOI: 10.1063/5.0147314. URL: https://doi.org/ 10.1063/5.0147314.
[7] P.-I. Schneider, N. Srocka, S. Rodt, L. Zschiedrich, S. Reitzenstein, and S. Burger. Numerical optimization of the extraction efficiency of a quantum-dot based single-photon emitter into a single-mode fiber. Opt. Express 26 (2018), 8479–8492.
[8] M. Stengl, P. Gelß, S. Klus, and S. Pokutta. Existence and uniqueness of solutions of the Koopman–von Neumann equation on bounded domains (2023). arXiv: 2306.13504 [math.AP].
[9] K. Volkova, J. Heupel, S. Trofimov, F. Betz, R. Colom, R. W. MacQueen, S. Akhundzada, M. Reginka, A. Ehresmann, J. P. Reithmeier, S. Burger, C. Popov, and B. Naydenov. Optical and spin properties of nv center ensembles in diamond nano-pillars. Nanomaterials 12 (2022), 1516. DOI: 10.3390/nano12091516.
[10] Y. Wang, L. Vannucci, S. Burger, and N. Gregersen. Nearunity efficiency in ridge waveguide-based, on-chip single-photon sources. Mater. Quantum Technol. 2 (2022), 045004. DOI: 10.1088/2633-4356/aca8e8.