Projections from Dynamic Programming Based Extended Formulations

We illustrate our approach by a shortest path problem. Let D=(N,A) be a directed graph on node set N = {0,...,n} with costs c(a), a ∈ A on the arcs. Of course, the shortest path problem on D can be solved in polynomial time, for instance with the Bellman-Ford algorithm, if D has no negative cycles. The Bellman-Ford algorithm finds the optimal solution by generating the shortest paths between all pairs of nodes i,j with at most k arcs for k=0,1,...,n. Hence, also the k-shortest path problem on D can be solved in polynomial time.

We are interested in facets of the associated path polytopes P(0,n) and P^k(0,n), that is, the convex hull of the incidence vectors of (0,n)-paths and (0,n)-paths of cardinality at most k, respectively. If D is an acyclic digraph, then P(0,n) has a simple characterization. In this case the flow conservation constraints and the nonnegativity constraints are sufficient to determine P(0,n). However, a complete linear description of P^k(0,n) defined on an acyclic graph D is unknown.

Applying the DP-approach to the dominant of P^k(0,n) one can derive at least a characterization of the facet defining 0-1-inequalities of P^k(0,n).

The extended formulation

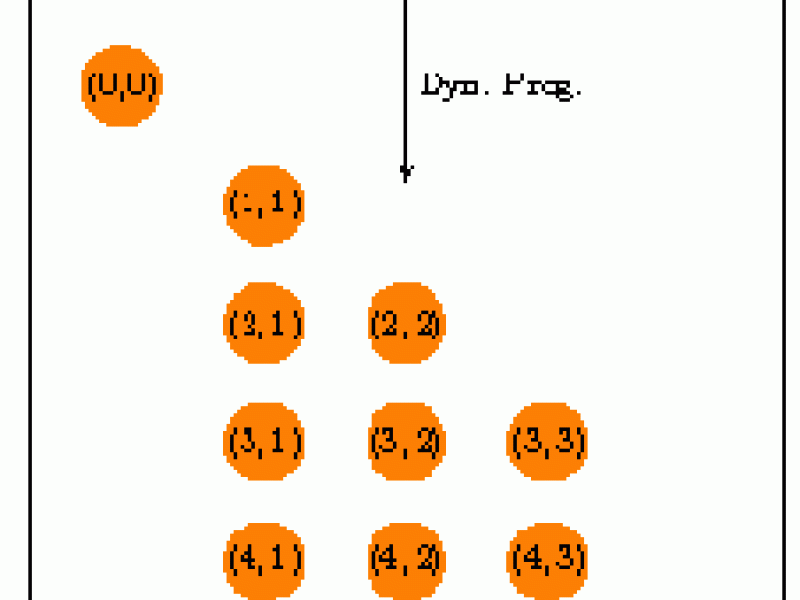
The dynamic programming approach provides an extended formulation of the k-shortest path problem in higher dimensional space. It transforms the cardinality restricted path problem on D into a non-cardinality restricted path problem on another acyclic digraph D' =(N',A') with start node (0,0) and target node (n,k). An illustration of this approach is shown in Figure 1.

The projection

Figure 2 encodes a ((0,0),(n,k))-cut of D' with partitions S and T. If a node is labeled with 1, it belongs to S, otherwise to T. The associated cut-inequality y(S:T) ≤ 1 is valid for the dominant of the path polytope P((0,0),(n,k)). This inequality can be identified with a valid 0-1-inequality bx ≤ 1 for the dominant of P^k(0,n). We identified all those ((0,0),(n,k))-cut inequalities y(S:T) ≤ 1 whose associated inequalities bx ≤ 1 in original space are facet defining for the dominant of P^k(0,n). Figure 2 shows one such ((0,0),(n,k))-cut.

Figure 1) DP-based extended formulation	Figure 2) Illustration of a ((0,0),(n,k))-cut