StableSets
Stable sets and special graph classes
Stable sets in graphs form one of the important models in integer programming and have various applications. However, the stable set problem is NP-hard and also not easy to treat in practice. The polynomial time solvability of the stable set problem is known for a few graph classes only. Among them, perfect graphs admit the most interesting structure since different characterizations of perfect graphs provide an interface between graph theory, polyhedral theory, information theory, and integer programming and reveal, thereby, insight in the relation of these areas. Perfect graphs are, e.g., characterized by means of graph entropy, the imperfection ratio of a graph can be expressed via the graph entropy, and the graph entropy by means of stable set polytopes - showing the interaction between the three concepts. The subject of this project within the framework of the DFG research group "Algorithms, Structur, Randomness" is to relax and generalize the concepts involved in the three characterizations of perfect graphs: Rank-perfect graphs form a superclass of perfect graphs w.r.t. the stable set polytope, normal graphs w.r.t. the graph entropy. The aim is to explore which of the important properties of perfect graphs these superclasses share. Moreover, in joint work with the project "Stable multi-sets" the study of stable set problem and polytope should be extended to the more general concept of stable multi-sets.
Rank-perfect and weakly rank-perfect graphs
The polynomial time solvability of the stable set problem for perfect graphs relies on a polynomial time separation algorithm for a class of inequalities containing all non-trivial facets of their stable set polytopes, the so-called clique constraints. Following a suggestion of Grötschel, Lovasz, and Schrijver (1988), one may relax the notion of perfectness by generalizing clique constraints to other classes of inequalities and investigating all graphs whose stable set polytopes admit such inequalities as only non-trivial facets.
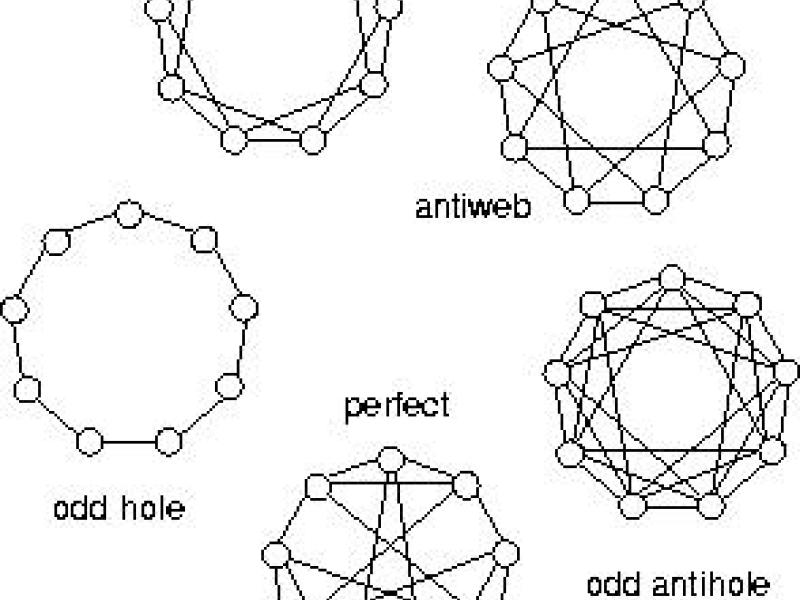
A natural generalization of clique constraints are so-called rank constraints and weak rank constraints, the corresponding superclassesof perfect graphs are the rank-perfect and weakly rank-perfect graphs, introduced by Wagler (2000). There are several classes of rank-perfect and weakly rank-perfect graphs known from the literature, see Wagler (2002) for a survey. In particular, the investigation of the stable set polytopes of graphs with circular structure, called webs and antiwebs, revealed that antiwebs are rank-perfect (Wagler 2003) whereas webs are far from having this property (see Pecher and Wagler 2003). It is an open question whether webs are at least weakly rank-perfect.
Normal graphs and the Normal Graph Conjecture
Normal graphs form an information theoretic superclass of perfect graphs and can be seen as closure of perfect graphs by means of co-normal products (Körner 1973) and graph entropy (Cziszar et al. 1990).
Perfect graphs have been recently characterized as those graphs without odd holes and odd antiholes (Strong Perfect Graph Theorem, Chudnovsky et al. 2002). In analogy, Körner and de Simone conjectured that the non-existence of the three smallest odd holes and odd antiholes implies normality (Normal Graph Conjecture, Körner and de Simone 1999). We showed that the Normal Graph Conjecture is asymptotically true and verified it for two first graph classes: webs and antiwebs (Wagler 2004). Proving or disproving the Normal Graph Conjecture in general is subject of our investigations.
Imperfection ratio and stable multi-sets
Recently both the imperfection ratio and the imperfection index of graphs has been studied and compared. In this context, also the extreme points of the clique relaxation of the stable set polytope have been revisited.
An evident generalization of stable sets are so-called stable multi-sets introduced by Koster and Zymolka (2002). In joint work with the project "Stable multi-sets", we focus on properties of the stable multi-set polytope as well as its linear relaxation, addressing both theoretical and computational aspects (see Koster and Zymolka 2003). Many of the results are motivated by known results for the stable set problem and provide a deeper insight to the latter.