Non-destructive testing and quality control in technology and civil engineering, as well as the continuous updating of digital twins, require the repeated solution of parameter identification problems to estimate the state of the system from measurements. These systems are often described by forward models in the form of parametrized systems of partial differential equations (PDEs). These include Maxwell’s equations in optical metrology applications, solid mechanics in bridge surveillance, and the heat equation for time-of-death estimation in forensic medicine.
Estimating the state parameters requires many solutions of these PDE systems in an optimization method for computing maximum posterior point estimates or in Markov-Chain Monte Carlo methods for sampling the posterior probability distribution. Each individual solution may require significant computational resources, often making the parameter estimation procedure too slow for real-time applications.
Replacing the PDE solver with a fast surrogate mod-el that maps parameters directly to the measurable outputs can bypass expensive simulations. Surrogate models using Gaussian process regression, neural networks, sparse grids, or polynomial interpolation are trained offline using data consisting of parameter–measurement pairs. Often, a large number of training data points are required, making the construction of surrogate models expensive. This cost is typically reduced by selecting the most informative parameters for acquiring training data. When computing training data via PDE simulations, there is an additional design choice: the accuracy with which to solve the PDE numerically.
Design of computer experiments
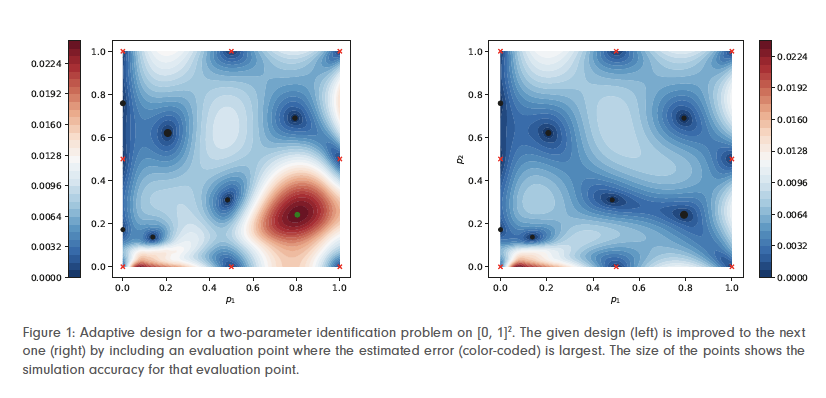
In collaboration with scientists from Friedrich-Alexander-Universität (FAU), Fraunhofer IISB, and Bundesanstalt für Materialforschung und -Prüfung (BAM), and supported by Bundesministerium für Bildung und Forschung (BMBF) and Deutsche Forschungsgemeinschaft (DFG), researchers at ZIB have developed adaptive algorithms for selecting both parameter positions and simulation accuracies for computing training data. The method aims to select a design D (a particular choice of parameter positions and corresponding simulation ac-curacies) minimizing the error introduced by the surrogate approximation for a given computational budget. It combines a posteriori error estimators E(D) for the surrogate model, as provided explicitly by Gaussian pro-cess regression surrogates, with a priori estimates of the computational effort W(D) required for solving the PDE up to the requested accuracies. In a greedy fashion, starting from a given design D, we seek an improved design D′ that can be realized with a small increment ∆W of computational budget – that is, we solve the de-sign of computer experiments problem

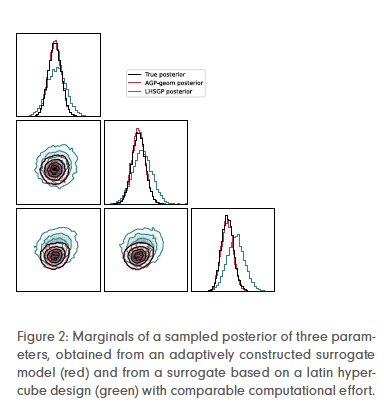
Depending on how the surrogate model is used – either for computing point estimates of the parameters or for sampling the posterior density – the introduced error propagates into different quantities of interest. Thus, the notion of error depends on the application. We have derived error estimators for two cases: first, for the deviation of reconstructed parameters relative to the uncertainty inherent due to measurement errors, and second, for the Kullback–Leibler divergence between the true posterior density and the posterior obtained when using a surrogate model (see Figure 2).
Significant performance improvements
Compared to a priori designs such as factorial designs, latin hypercubes or low-discrepancy sequences, and even compared to adaptively selected parameter positions with fixed simulation accuracy, the additional adaptive choice of accuracies significantly improves the efficiency of surrogate model creation. In both simple test examples and actual PDE inverse problems, the required computational effort for training data simulation has been reduced by a factor of ten or more (see Figure 3). This is particularly true if gradients of the forward model can be cheaply evaluated.