Dynamic (4D) live imaging of cellular processes provides a wealth of data. In order to gain biological insight, the observed processes need to be quantified and therefore subcellular structures in the image data to be tracked. This reconstruction task is a challenging task currently done semi-automatically with huge manual effort. In this project we aim at reducing the required human labour by using quantitative models of growth cone and filopodia geometry and dynamics for a more robust and consistent algorithmic identification of subcellular structures.
Data description
- Brain development of flies (Drosophila) is being observed through 4D (3D + time) 2-photon microscopy
- 60 timesteps over 1h including multiple growth cones
- Filopodia are attached to a growth cone
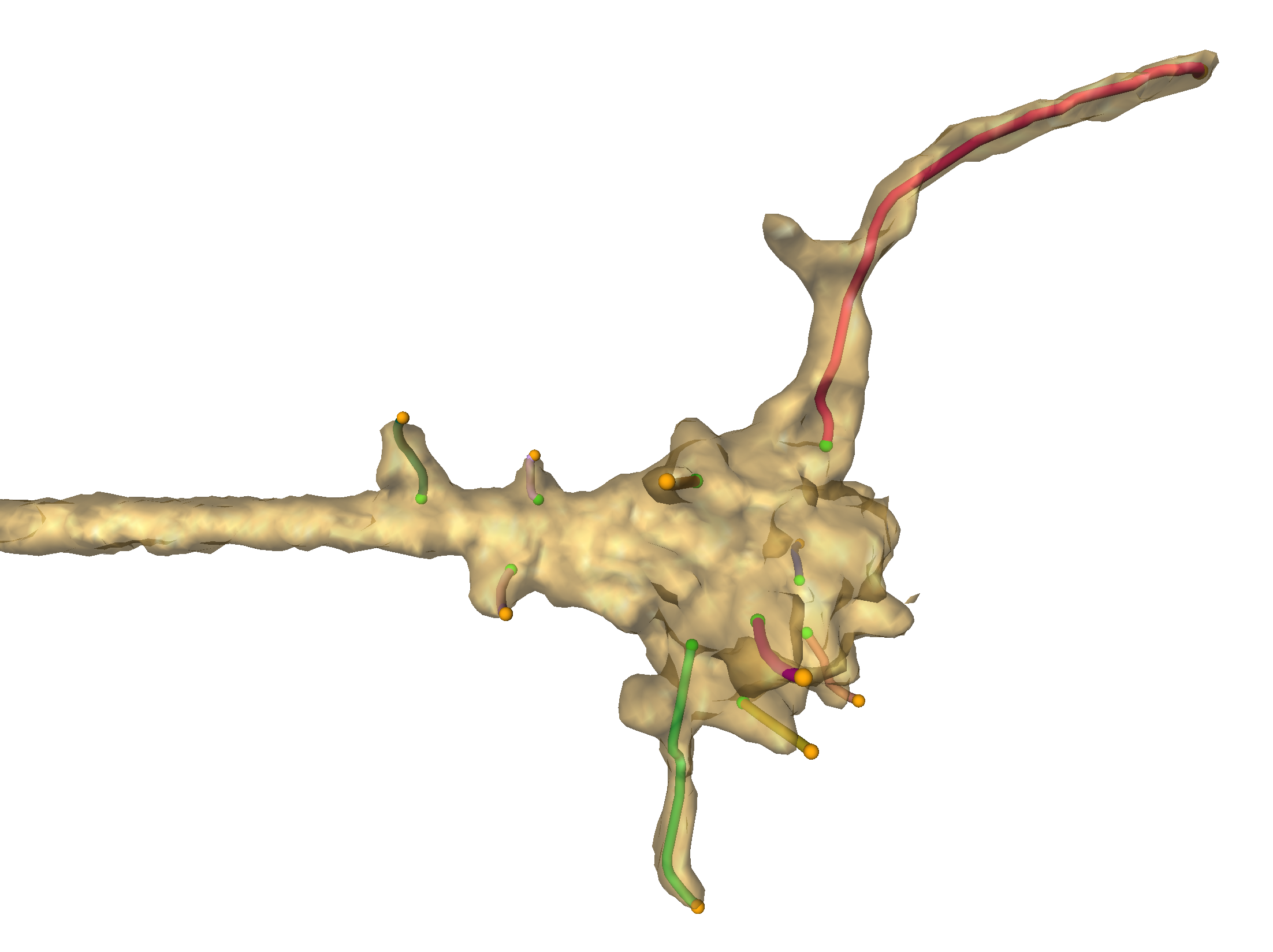
Fig 1. Transparent surface visualization of a growth cone and corresponding axon (on the left side) for one timestep. Filopodia reconstructions are represented as colored lines, e.g. the red line in the top part.
Goal
Dramatic increase of image analysis throughput by model-based filopodia segmentation and tracking compared to semi-automatic reconstruction algorithm previously created at ZIB (project Analysis of Growth Cone Dynamics)
Main framework
Use Bayesian inference methods for filopodia reconstruction and tracking that can respect user-provided constraints. Here, the prior compares a potential filopodia model to previously known filopodial length dynamics while the likelihood term compares the model to the dataset at hand.
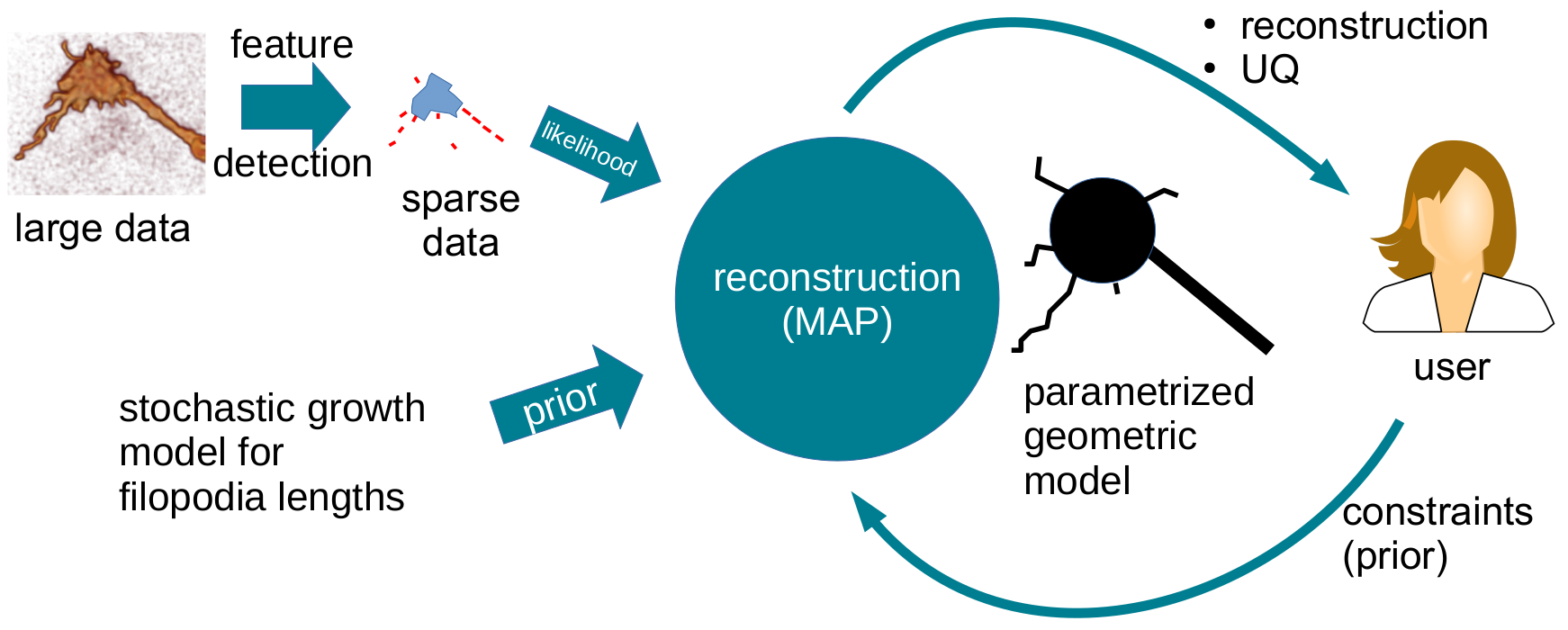
Fig 2. Schematic illustration of Bayesian reconstruction framework.
Prior
Stochastic models based on reconstructed data (using the semi-automatic algorithm) are available for filopodial growth and for synapse formation, and were created in the ZIB project Stochastic pattern formation in brain wiring. Here, only the growth dynamics are relevant and the previous stochastic model is currently being replaced by modeling the conditional length distribution (dependent on the length in previous timestep) as a sum of Laplace distributions with an exponential vanishing probability.
Likelihood
We use reconstructions generated by the semi-automatic algorithm as training data for a U-Net based Deep-CNN semantic segmentation of filopodia (using individual 3D images, so time dependencies are not taken into consideration). Currently, we follow the U-Net variation described in Brain Tumor Segmentation and Radiomics Survival Prediction: Contribution to the BRATS 2017 Challenge by Isensee et al.

