During brain development, synaptic connection patterns are formed in an extremely robust manner. As the interconnection patterns are much too complex to be encoded directly in the genome, they must emerge from simpler rules. In this project we investigate mechanistic stochastic models of axon growth and filopodial dynamics, checking whether their simulation leads to connection patterns and dynamics as observed in vivo, and with the same robustness.
During the development of the brain, the neurons form specific patterns in a very robust and
reliable way. The question of how the axons and dendrites find the appropriate synaptic partners
has been studied for decades, but is posed today with a new twist.
Axon guidance revisited
For the last 70 years, the dominant model of axon guidance due to R. Sperry have been global
concentration gradients of guidance molecules, of which about 100 different species are known
today. During axon growth -- filopodia, small extrusions of the growth cone -- sprout in different
directions, as has been observed in histological microscopy images. The general assumption
has been that the filopodia sample the surroundings for the chemical gradients of guidance
molecules, allowing to find the right direction despite the stochasticity of filopodia growth and
molecule sensing.
With the new technology of multi-photon time-lapse microscopy, the biologist R. Hiesinger (FU)
is able to acquire in vivo 4D microscopy movies of axons growing in drosophila brains -- and
sheds new light on axon guidance and the brain wiring process. The filopodial dynamics features
a much richer structure than would be necessary for stochastic gradient sampling (Figure 1).
Currently, the role that this complex dynamics plays in the brain wiring process is essentially
unknown.


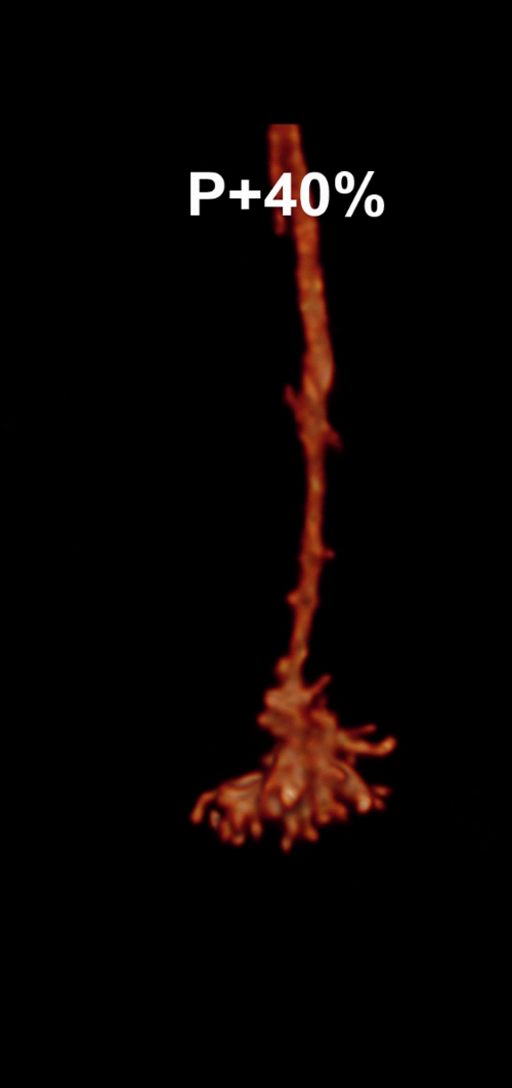
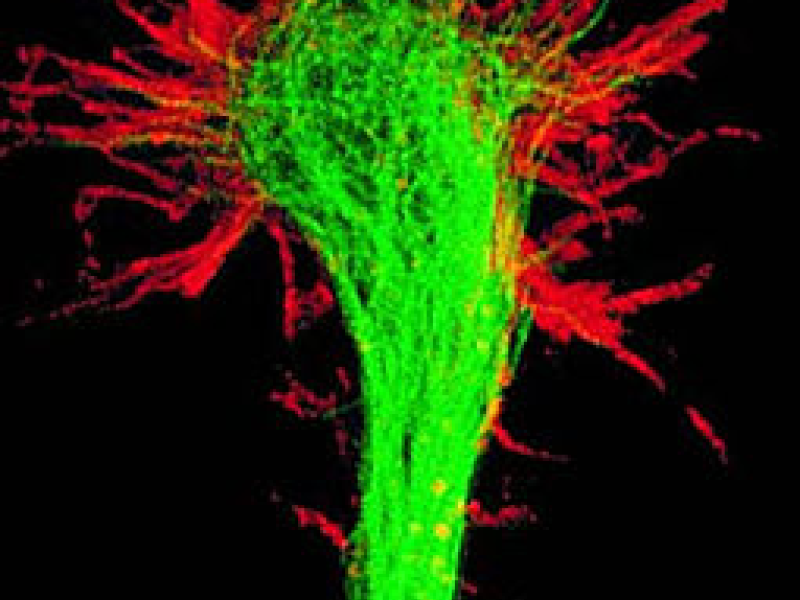
Figure 1: Snapshots of filopodia sprouting from an axon’s growth cone at different times during
the drosophila brain development. Data courtesy R. Hiesinger.
Looking for simplicity
The drosophila genome is too small for encoding the brain wiring explicitly. Thus, the pattern
must emerge from rather simple regulatory mechanisms that are encoded in the genome [1].
One compelling hypothesis is that these developmental rules do not only tolerate randomness in
the axons’ environment, but use stochasticity as a driving force and to achieve robustness.
In a joint MATHEON project with M. von Kleist (FU), we aim at identifying mechanistic models
that are both physically plausible and able to reproduce observed wiring patterns and the
statistics of filopodial dynamics (Figure 2). The simpler and more general the mechanisms
forming such a model can be, the more one can expect that structurally similar processes are
actually driving the neural development.
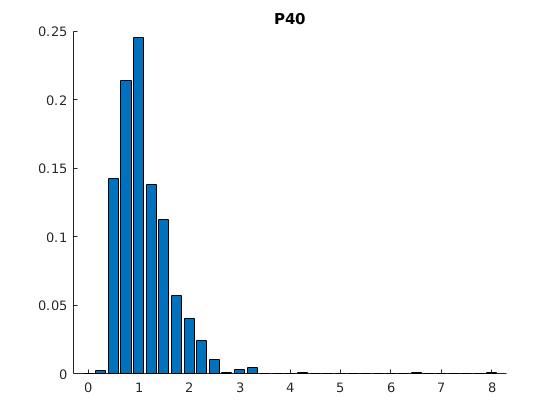
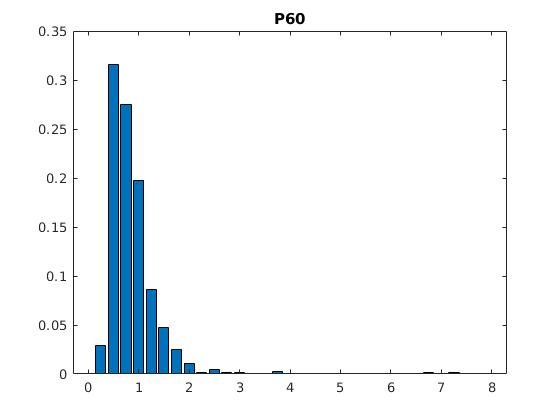
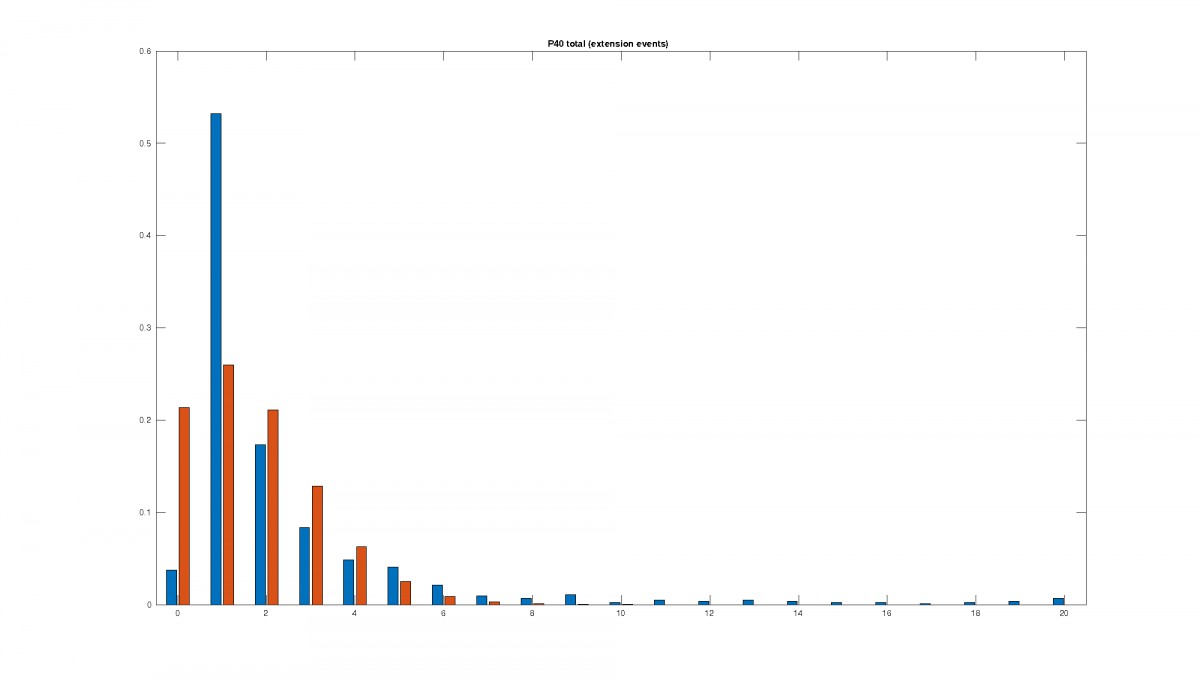
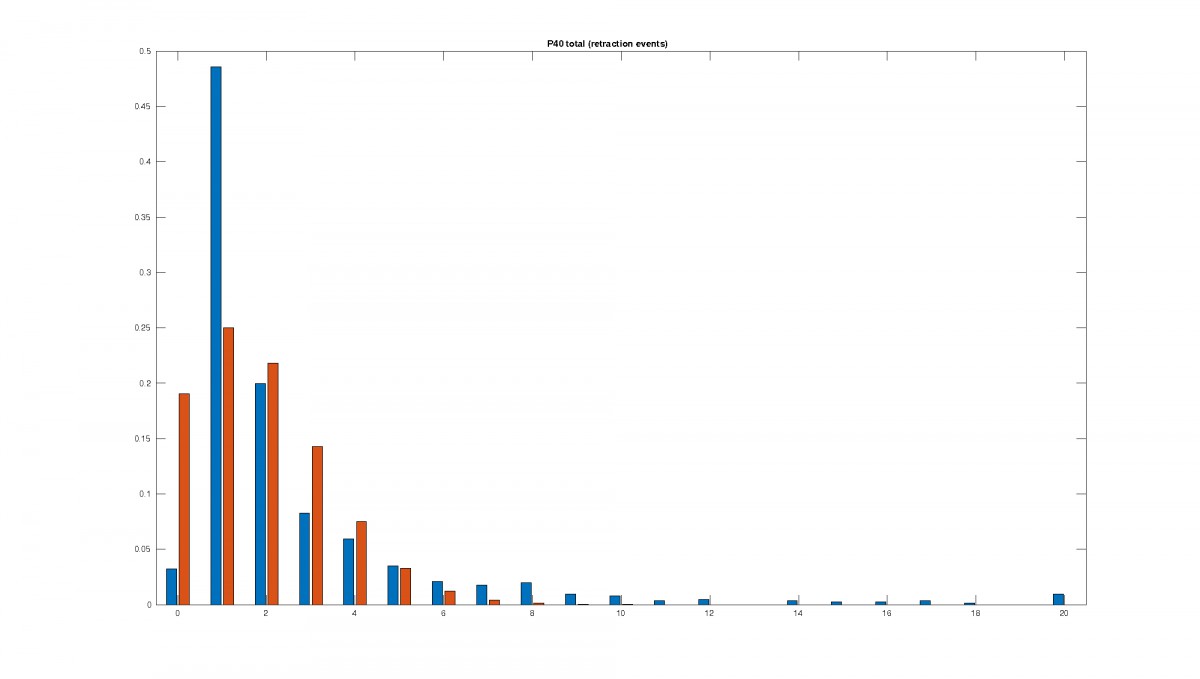
Figure 2: Statistics of filopodia dynamics extracted from 4D microscopy data. Characteristic quantities
such as filopodia length (histogram of lenghts taken from an hour of observation at P+40% and P+60%)
filopodia extension and retraction events follow a Poisson distribution.
Stochastic simulation algorithms coupled to partial differential equations
As a first candidate, we consider a model comprising three essential components. First,
diffusion and decay of guidance molecules in the extracellular space seems necessary for inter-
axon communication. Reception of guidance molecules by the filopodia is probably a stochastic
process due to the low concentration. And finally, nonlinear reactions going on within the axons,
and affected by the sensing of guidance molecules, control growth and retraction of filopodia as
well as eventually the release of guidance molecules [2]. Intracellular diffusion and directed
transport may also play an essential role.
For simulating realizations of such models, solvers for deterministic partial differential equations
describing diffusion, reaction, and transport processes need to be coupled to a stochastic
simulation algorithm capturing the random events of guidance molecule reception and filopodia
growth.
Model complexity can be measured in terms of the number of involved species of guidance
molecules, and the number of nonlinear reactions. One of the simplest models of this type,
containing just a single type of guidance molecule, can already create robust and quasi-regular
space-filling axon structures that avoid self-contact as well as neighbour contact.
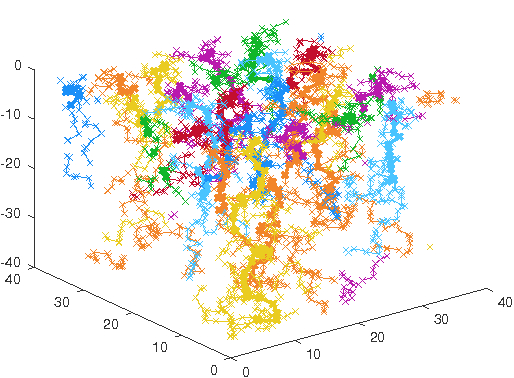
Figure 3: 25 axons in a spatially periodic setting growing to a robust and quasi-regular space-
filling pattern.
For the stochasticity in the model, the statistics for length, lifetime, extension and retraction events
as well as birth and death rate such as in Figure 2 are evaluated.
They are used in a Gillespie or chemical master equation algorithm, to test and find the transition
propensities for a filopodium to become a bulbous tip on synapse partner contact (reversible) and
for a bulbous tip to become a stable synapse (irreversible), cf. Figure 4.
Irrespective of the bulbous tip forming a synapse or forming back to a filopodium, on becoming a
bulbous tip, a feedback to the axon's growth cone takes place, that inhibits the filopodial activity.
This regulates observably the number of synapses being formed.
It has also been found, that should molecules 'DLar' or 'Liprin-a' (read alpha) be missing, the
feedforward from bulbous tips to become synapses (Figure 4, green arrow) is inhibited rendering
less synapses. Should the molecule 'trio' be missing, the feedback to filopodial dynamic reduction
is flawed, which leads to more observed bulbous tips than in the wild type axon. The molecule
'Syd1' has an impact on both feeds.
The effect of these molecules is also to be included and tested in the model. Found transition
propensities will then be transferred to the geometric model (Figure 3) and cross checked to
find what role spatial distribution plays or how synapse partners need to be spatially distributed
in order to achieve the same propensities.
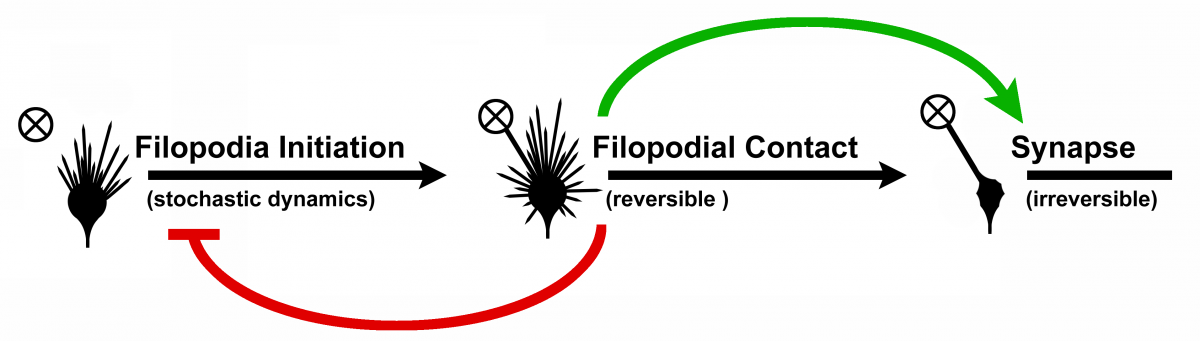
Figure 4: Transition model from filopodium to synapse. On filopodial contact so-called bulbous tips
are formed, on which the filopodial dynamics is damped (red feedback). The bulbous tips can either
stabilize and become synapses or transition back to a filopodium. Novel model developed by
R. Hiesinger et. al.
References:
[1] B.A. Hassan and P.R. Hiesinger. Beyond molecular codes: Simple rules to wire complex
brains. Cell 163:285–291, 2015.
[2] C.-C. Chan, D. Epstein, R. Hiesinger. Intracellular Trafficking in Drosophila Visual System
Development: A Basis for Pattern Formation Through Simple Mechanisms. Dev. Neurobiology
71:1227-45, 2011.
[3] M.N. Özel, A. Kulkarni, A. Hasan, J. Schallau, M. Moldenhauer, I.-M. Daumann, H.
Wolfenberg, V.J. Dercksen, M. von Kleist, M. Weiser, et al. (in preparation). Co-regulation
of axon filopodial dynamics and synapse formation by presynaptic early active zone
components.