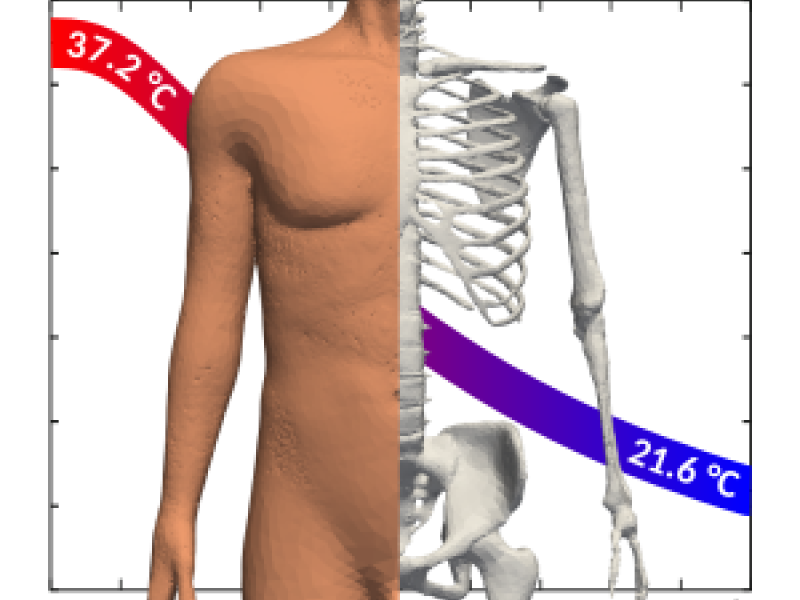
In forensic medicine, accurate determination of time of death remains a critical component in solving violent crimes. The prevailing technique relies on tracking the decrease in body up to 2-3 days after the victim's death. Although this method, which relies on empirical parameterized cooling curves, takes into account factors such as body mass, ambient temperature, and clothing, it often struggles to account for the wide variety of thermal situations encountered in the real world.
To overcome these limitations, our ongoing project focuses on researching and implementing mechanistic time of death estimation (TDE) methods. These methods rely on the mathematical description of physical heat transfer processes to provide a more accurate representation of various cooling scenarios. This approach promises a higher degree of objectivity as it relies on physically parameterizable quantities.
Our project involves solving an inverse problem related to the heat equation - a partial differential equation that determines how heat propagates through a region over time. This forms the basis for understanding how the temperature of a corpse changes after death. We create highly detailed 3D grids for our simulations by processing CT scans of the corpse using the ZIBAmira software and the CGAL library. The different tissue types are identified and segmented to obtain an accurate representation. This segmented data is then converted into a tetrahedral mesh that is the foundation for our heat transfer simulations.
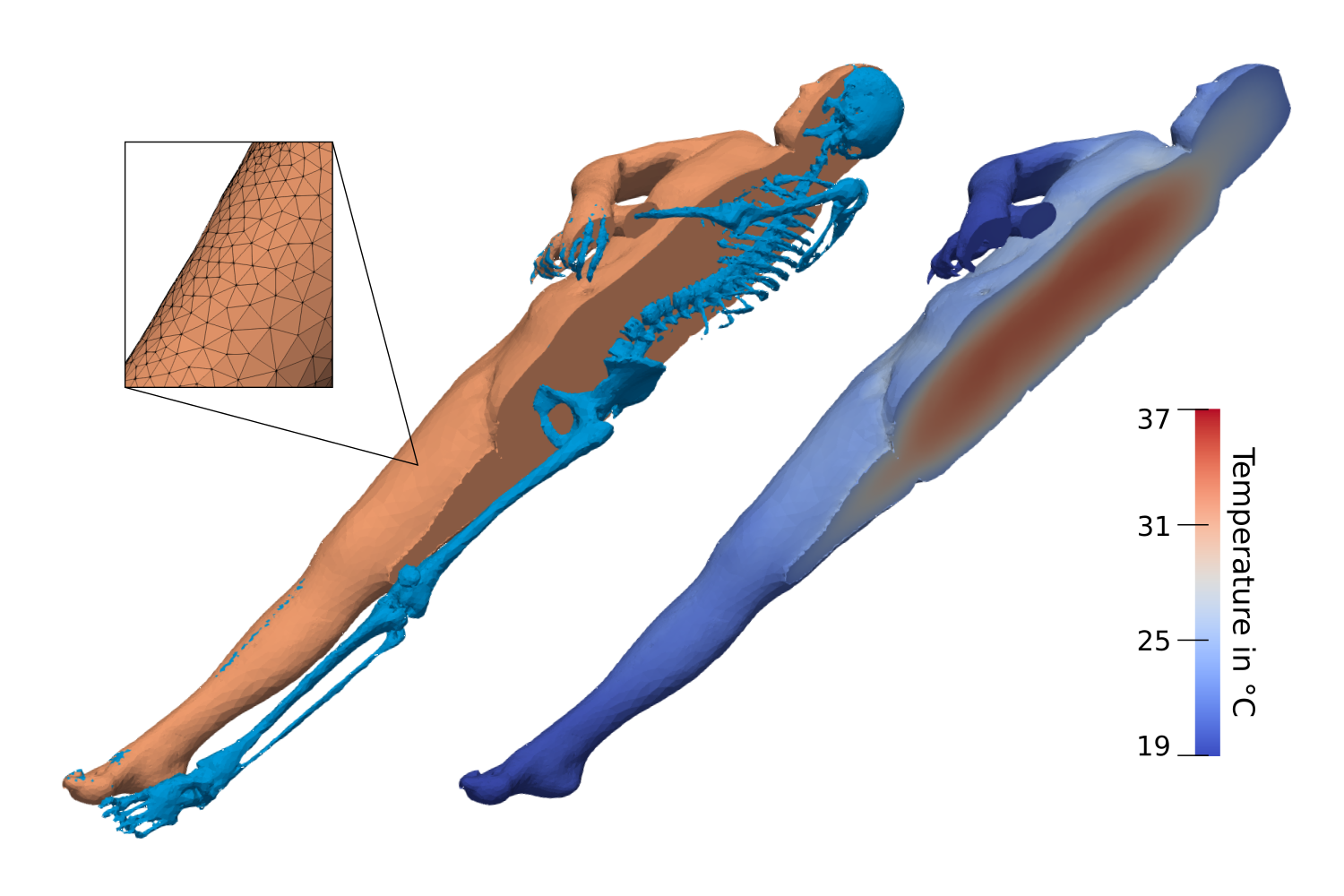
Fig. 1: CT-generated body geometry as a tetrahedral grid with different tissue types (here using the example of bones) as well as FE simulation of cooling
Central to our project is the gradient-based solution of the inverse problem for the heat equation, implemented via the Kaskade7 toolbox,
- to minimize model-data mismatch,
- to quantify uncertainties of thermal parameters and
- to identify distributed parameters, best parameterizations and sensitivities.
Throughout the project, we have made significant progress in various areas:
Parameter Sensitivities
The parameters of the heat transfer equation for a corpse are often not precisely known, so a sensitivity analysis with respect to the thermal tissue parameters (like heat capacity, conductivity or heat transfer coefficient) is required to determine the most influential factors. Our analysis found that ambient temperature rates and fat and muscle tissue, along with heat transfer at the boundary, had the greatest influence on the estimate of time of death. Likewise, it was found that a highly accurate and detailed representation of the anatomy is not essential. Instead, accurate recording of the total volume of tissues with dominant water or fat composition and their overall geometric location is critical.
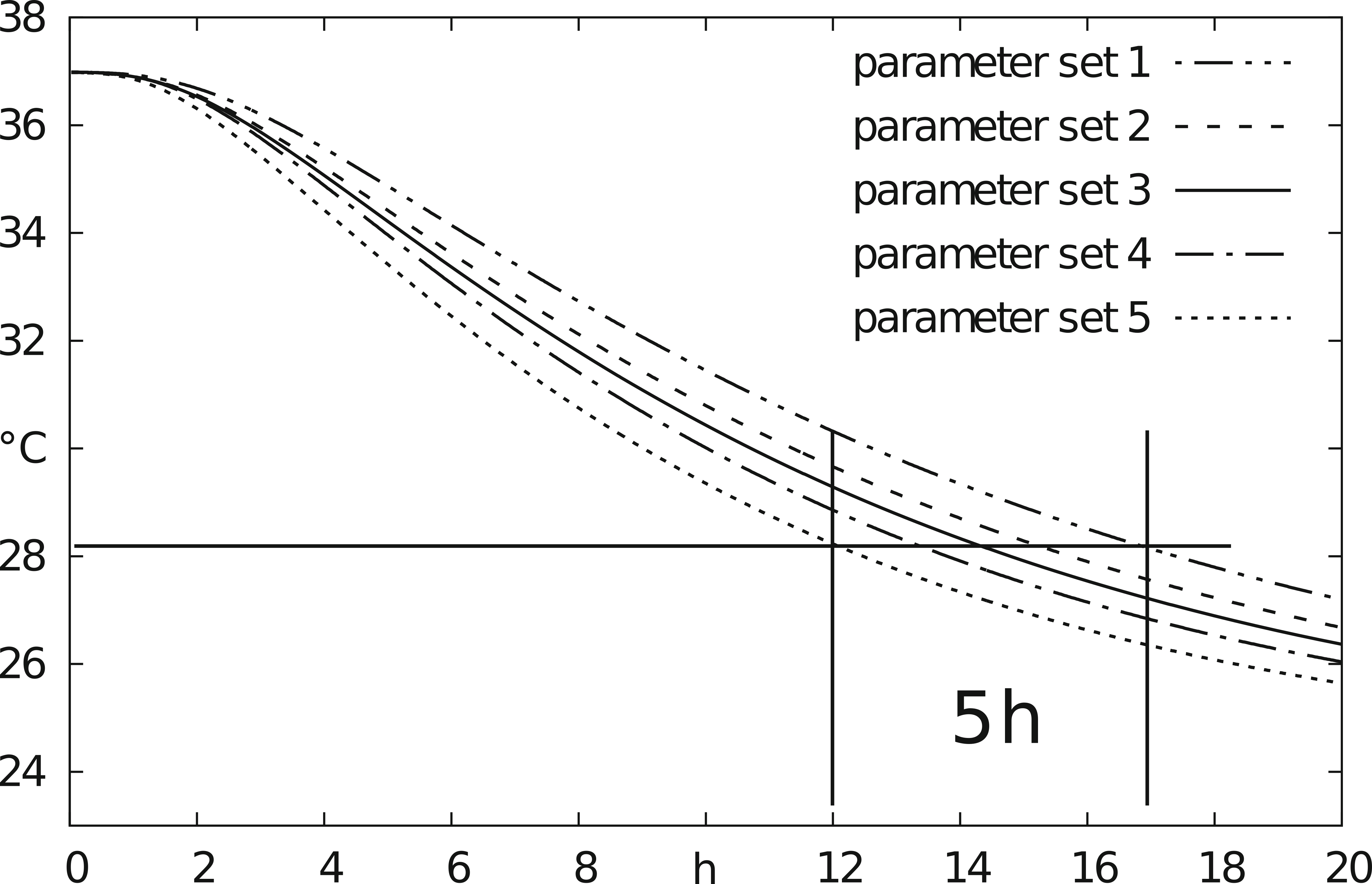
Fig. 2: Cooling curves for different parameter sets from FE simulation, leading to significant deviation in time of death
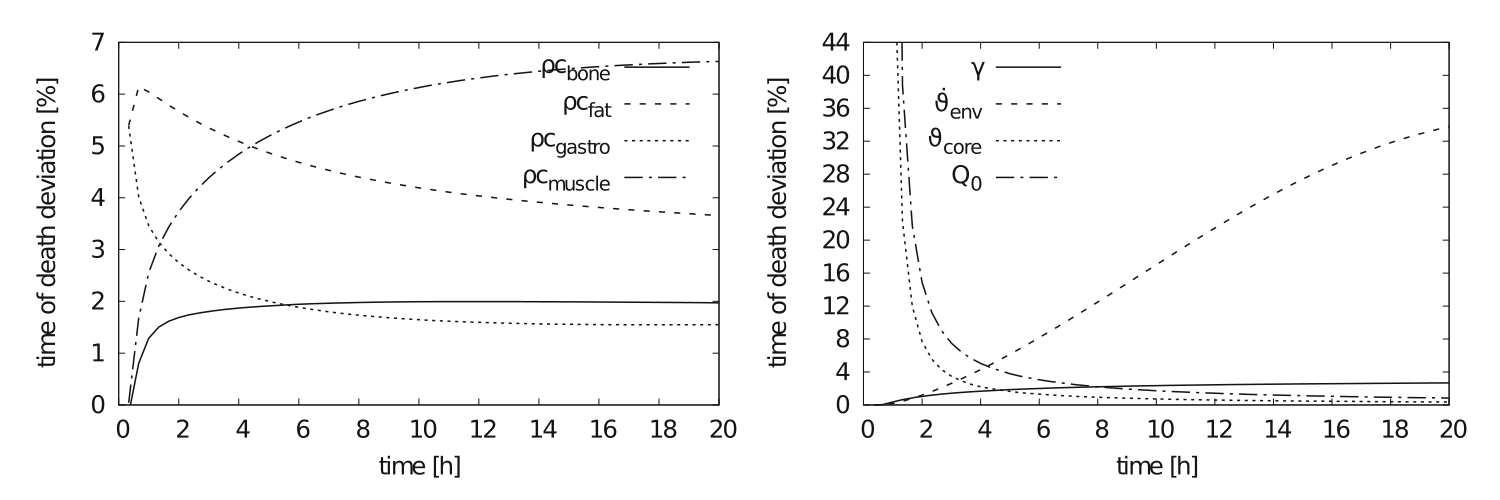
Fig. 3: Parameter uncertainty impact for tissue heat capacity (left) and for the global parameters effective heat transfer coefficient, environmental temperature rate, initial core temperature and supravital heating by metabolism
Contact Mechanics
Different underlying surfaces, whether insulating or cooling, can influence the effective heat transfer coefficient, thus affect the body's cooling rate and consequently the estimation of the time of death. Our work investigates how surface characteristics, such as material hardness, impact these calculations.
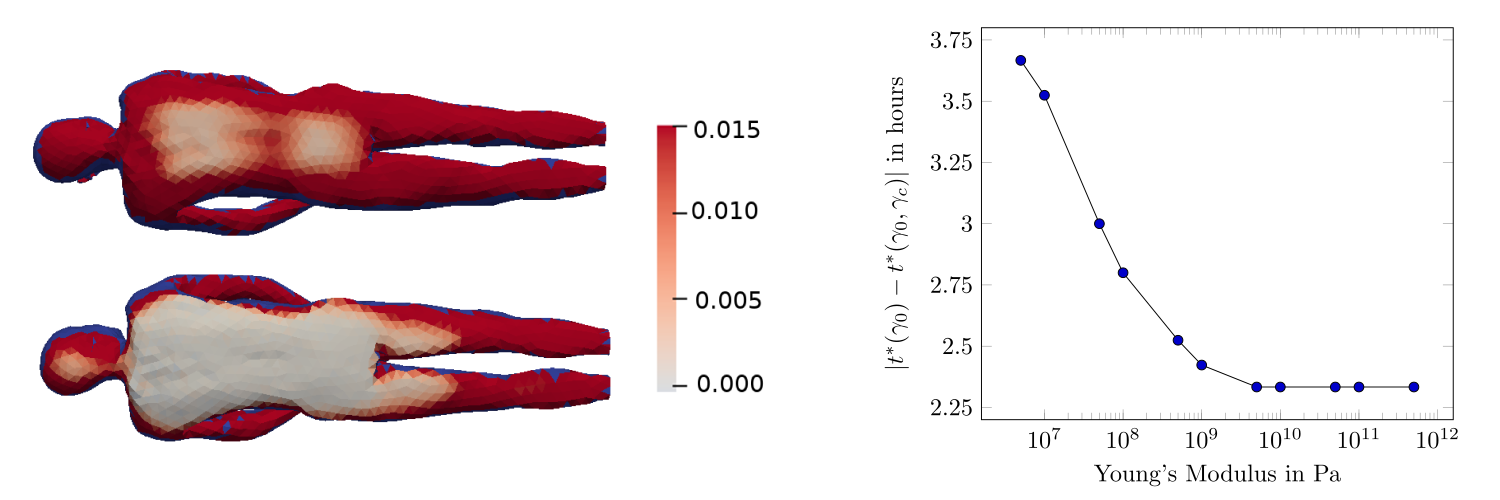
Fig. 4: Value of gap function g shows contact surface and hard vs. soft underground (left), difference of time of death considering materials of different hardness by Young‘s modulus (right)
Radiative Boundary
Radiative interactions play a notable role in the cooling process, especially in areas where the body surfaces are close together, such as parallel thighs, drawn-up legs, or arms positioned over the pelvic area. We model these interactions through heat transfer coefficients and view factors. Despite not being a dominant factor, the effect of heat radiation, as shown in both experimental and simulation studies using two closely spaced polyethylene (PE) cylinders cooling in the climate chamber, is quantitatively significant.
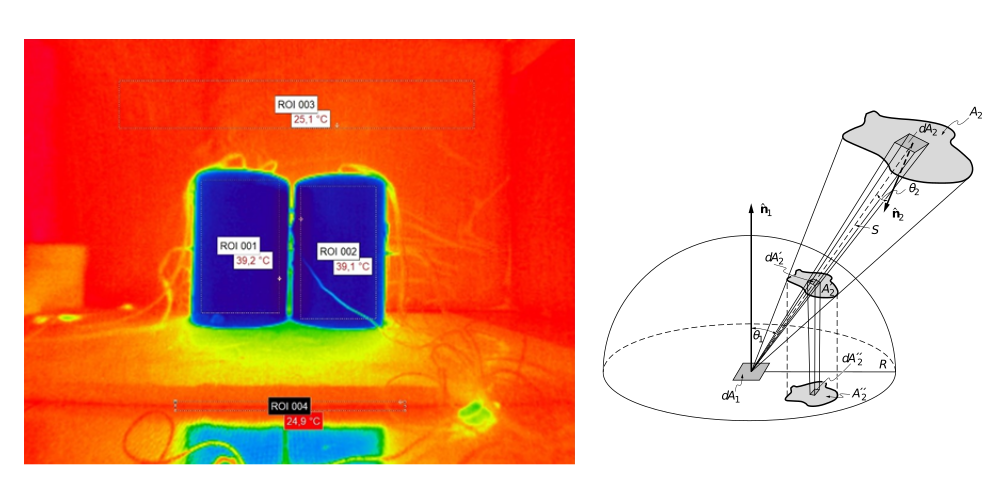
Fig. 5: Still image from the infrared camera: Cooling of two PE cylinders in the climatic chamber, cylinder positioned on Styrofoam plate (left), Nußelt view factors (right)
Natural Convection
Natural convection involves modeling air motion and heat transfer around a corpse in enclosed spaces, using the Navier-Stokes and heat transfer equations. It considers significant buoyancy forces due to temperature differences, leading to turbulent flows despite the minor temperature changes during corpse cooling. This approach provides a comprehensive understanding of fluid dynamics and thermal interactions near the corpse.
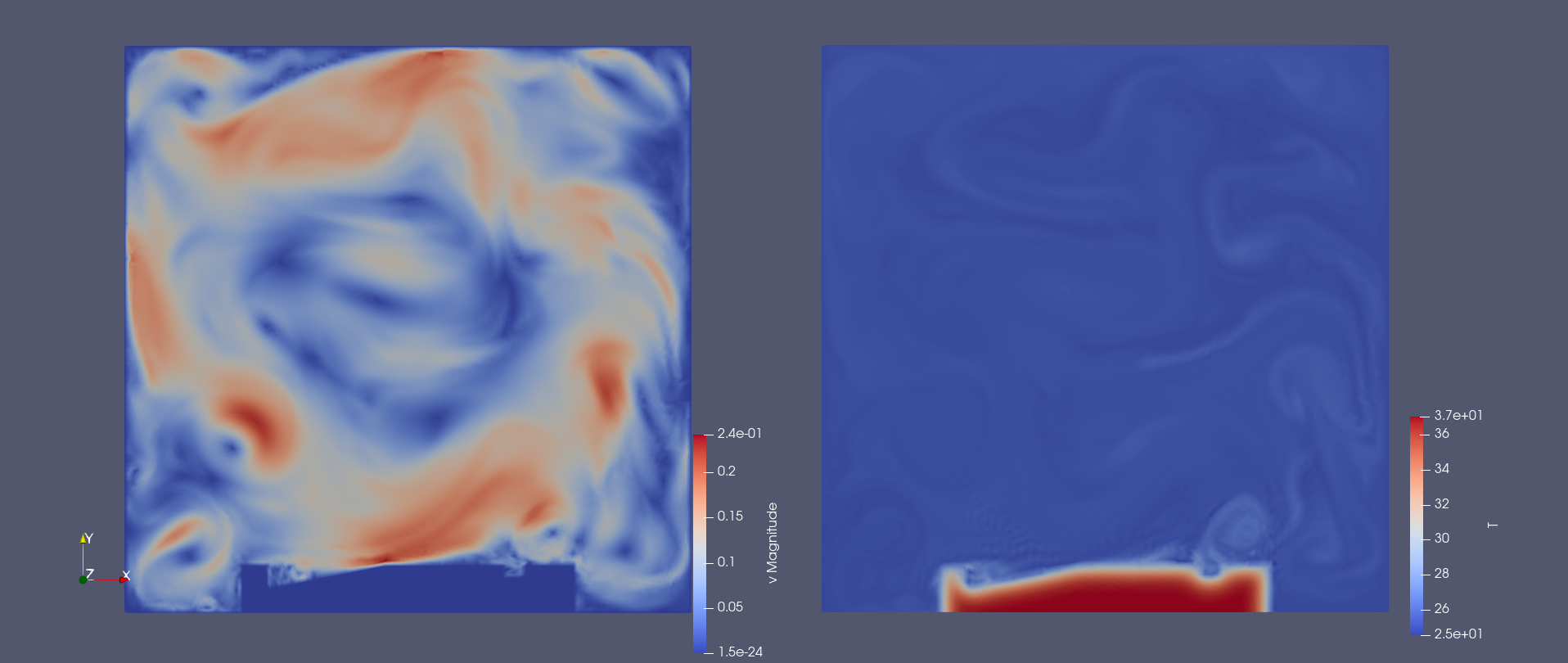
Fig. 6: Visualization of 2D simulation results on a lying corpse: flow rate (left), temperature (right)
Measurement Positions
We take into account that time of death estimation based on a single rectal measurement can be influenced by variations in measurement positions due to forensic investigation practices and anatomical differences. We understand that variations in thermometer insertion depth can lead to discrepancies of 2-3 hours in TDE within the first 45 hours post-mortem.
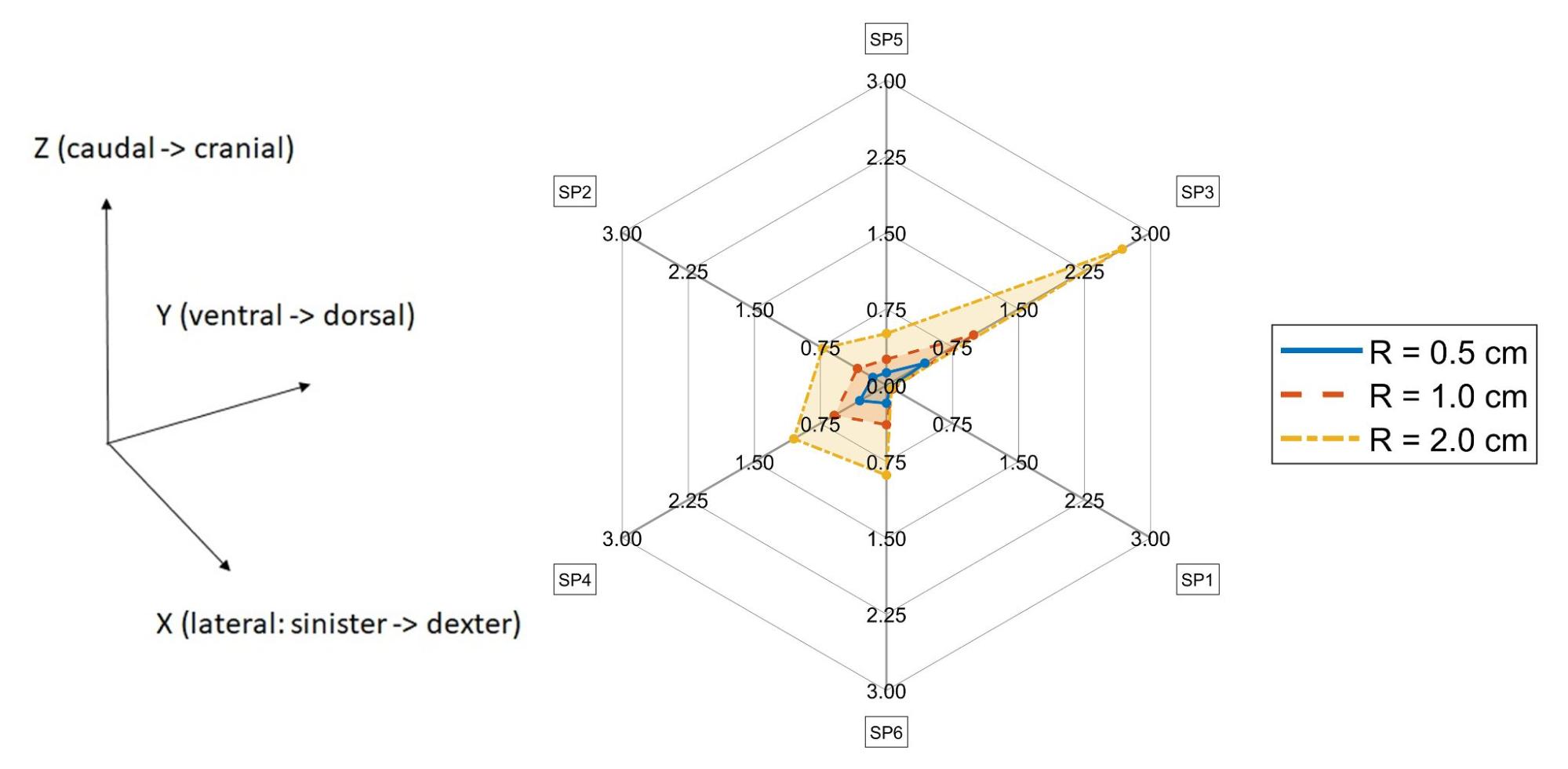
Fig. 7: Discrepancy in time of death for measurement positions with different radii around a reference position, especially in dorsal direction
Anatomical Factors
Anatomical variations affect time of death estimates significantly, with deviations of at least 5–10% emerging even after factoring in variations in body height, mass, and measurement location. This suggests that a single standard anatomy is insufficient for physics-based time of death estimation. To account for this, the use of a predefined set of template meshes, covering sex-specific tissue distributions and different body statures and shapes, is suggested.
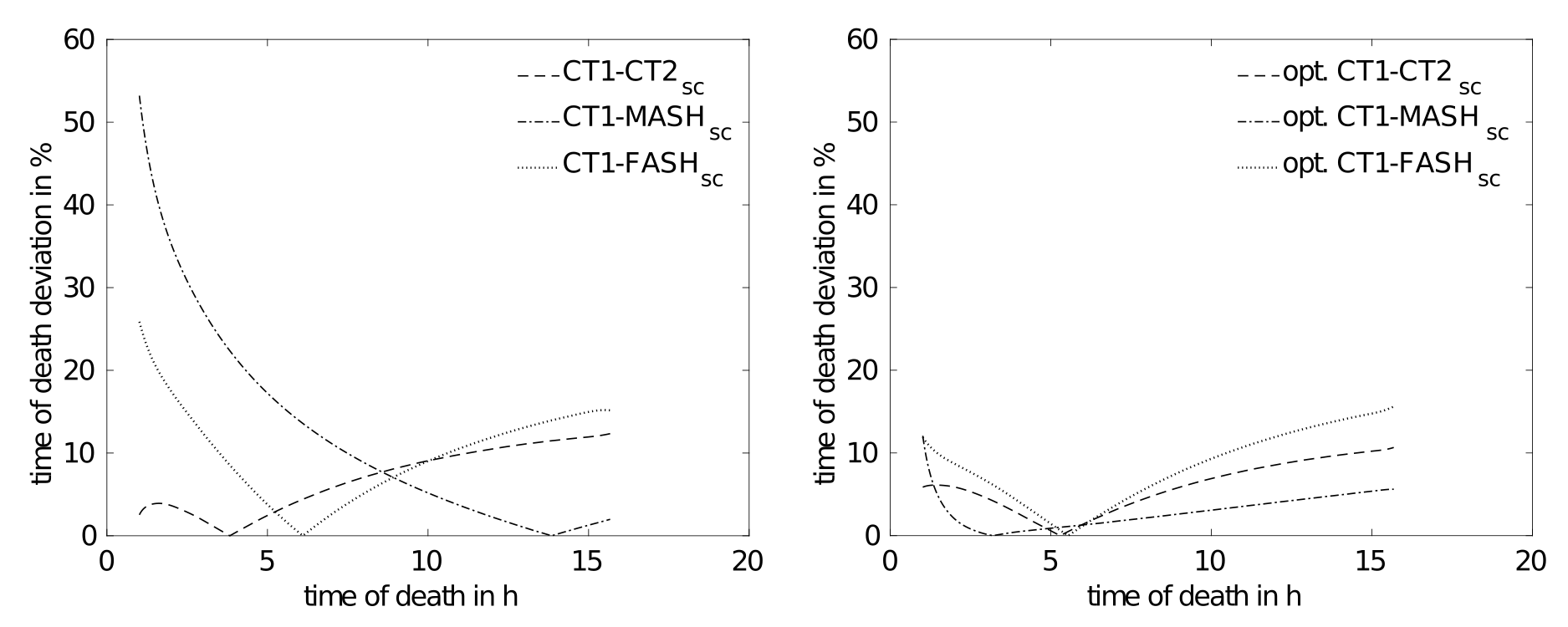
Fig. 8: Relative deviation of time of death for reference and optimized measurement positions w.r.t. CT1 model
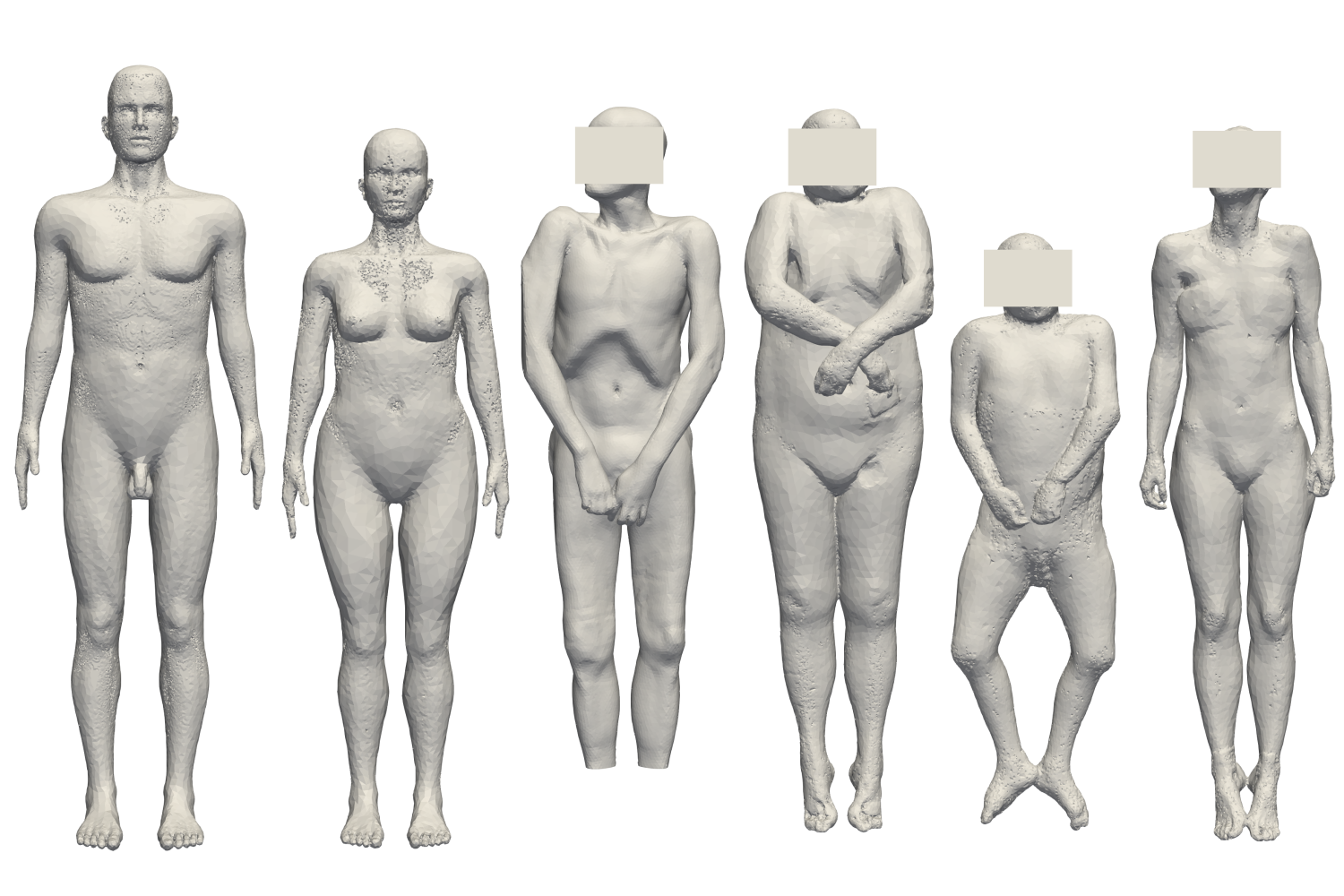
Fig. 9: Different 3D meshes obtained from CT scans and CAD design
Geometric Reduction
Geometric reduction involves the use of the BFGS algorithm and adjoint method to estimate distributed parameters essential for heat transport simulation. This approach allows identifying areas of the corpse model that can be neglected or simplified to reduce computational effort, a process known as Geometric Reduction of the Finite Element model (GRFE). The significance of local geometry decreases with distance from the measurement site, thus providing an opportunity to simplify remote parts of the model without significant precision loss.
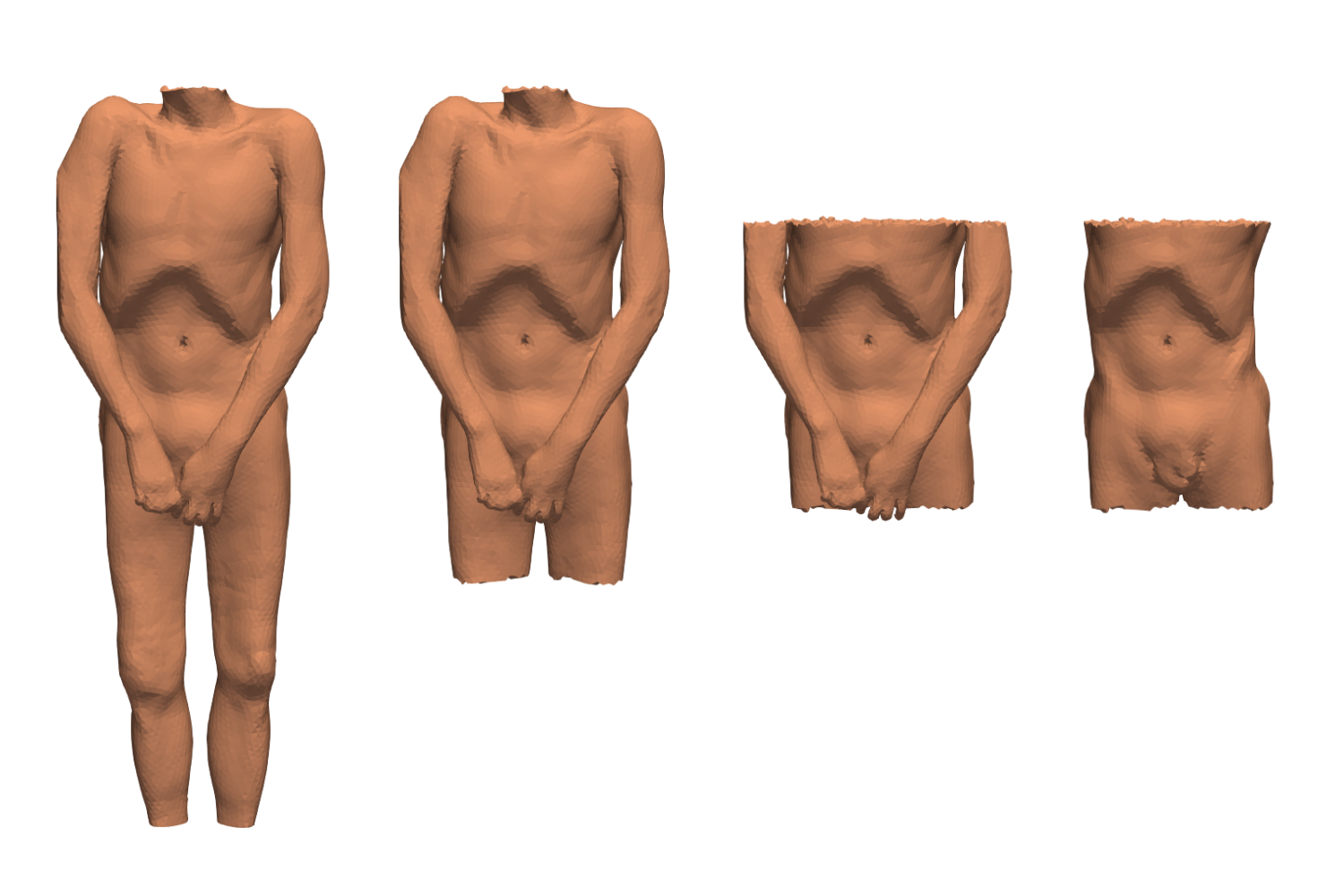
Fig. 10: Reduction of model complexity by cutting off potentially unnecessary parts of the model