The Tropical Geometry of Periodic Timetables brings together the mathematical optimization of periodic timetables, a key problem in the planning of public transportation of system, and tropical geometry, a discipline of pure mathematics situated on the intersection of algebraic geometry and discrete mathematics.
The fundamental connection between the two worlds is that a periodic timetabling problem, modeled by means of the Periodic Event Scheduling Problem (PESP), decomposes into minimum cost network tension problems over special polyhedra, namely polytropes. These are convex polytopes that are also tropically convex. This enables a dictionary between classical notions and techniques in periodic timetabling on one side, and features of tropical convexity on the other. The aim of the project is to make use of this dictionary to gain new insight into periodic timetabling algorithms, e.g., tropical neighborhood search, tropical coarse-to-fine methods, or tropical branch-and-bound.
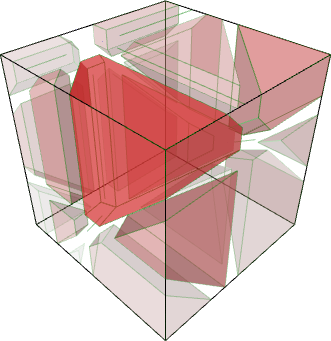
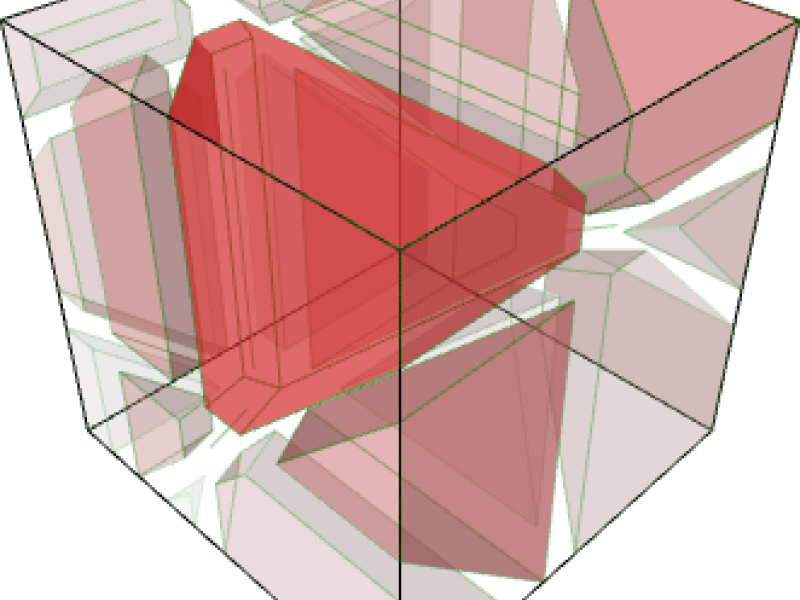
The image (credits: Enrico Bortoletto) shows a 3D decomposition of the space of feasible periodic timetables into red 3-dimensional and green 1-dimensional polytropes. There are, after preprocessing, no codimension 1 polytropes. The less transparent a polytrope is, the better is the total passenger travel time of the best timetable that it contains.
The project is funded by the Berlin Mathematics Research Center MATH+ and belongs to the MATH+ Application Area 3 Networks.