WHAT IS THE NEXT KEY INNOVATION?
Traffic and transport have always been key industries in the history of mankind. Progress often came from revolutionary innovations in vehicle technologies such as domesticated animals, the wheel, sailing ships, railways, subways, cars, and aircraft, as well as from the buildup of corresponding infrastructure networks and suitable organizational structures with which the transportation problems of their time could be solved, see Fig. 1.
»A model that might have taken a year to solve 10 years ago, might now solve in less than 10 seconds.«
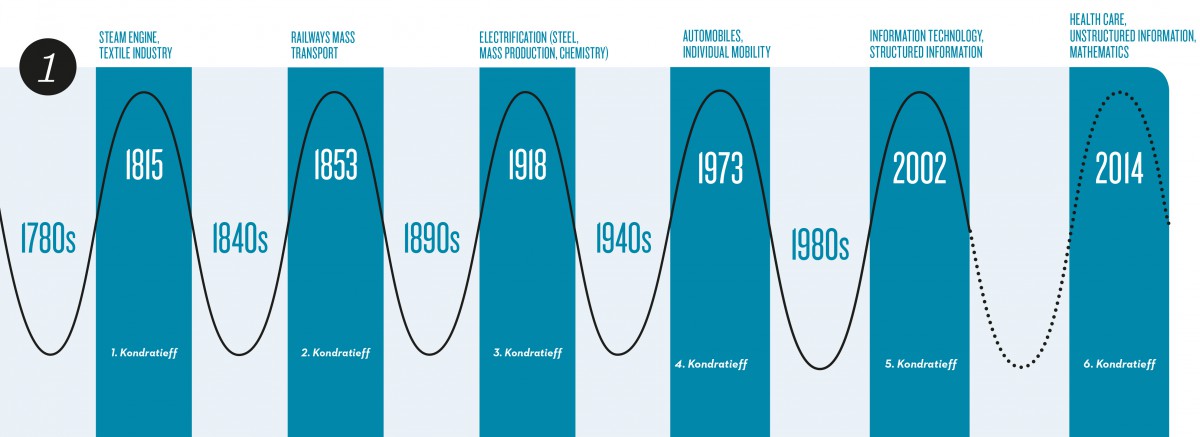
Several (Kondratieff)waves of innovations here triggered by progress in traffic and transport.
TODAY’S TRANSPORTATION CHALLENGES
These arise from urbanization, ageing societies, and a general scarcity of resources, including environmental ones. More than half of the world population already lives in cities, more will, and everybody has witnessed chaotic traffic situations in the megacities of Asia, America, or Africa. In Europe, people also move into the cities, depopulating the countryside, with mostly elderly peoplestaying. In general, costs for traffic and transport are rising, and people complain about congestion and pollution.
WHAT CAN WE DO?
It would be great if a technological breakthrough like a teleporter would come to our rescue, but this is unlikely − and we also do not need it! We witness significant progress on improving the efficiency of the existing vehicle technologies by downsizing engines, new fuels, better aero-und hydrodynamics, and by using modern information technology for trip planning and route guidance, online information, and internet ordering. In fact:
The existing means of transportation could be extremely efficient, if their system advantages would be put to use and the disadvantages could be avoided.
All we need is to make efficient use of these technologies, and the key to this is mathematics and information technology.
WHY MATHEMATICS CAN IMPROVE TRAFFIC AND TRANSPORT
This is actually an old dream, at least 100 years old. Nobel laureates like LeonidKantorovich and Tjalling Koopmans had it, and operations research was the discipline that tried to put it into practice in the 1960s. We know it didn’t work that time. But things have changed. Modern IT can provide all needed data and control. Computing power has increased dramatically. And what is not widely known: mathematical algorithms have improved at least as much as CPUs. Progress in computing speed and algorithms multiplies, making it now possible, for the first time in history, to solve large scale transportation problems to proven optimality. Traffic and transport are particularly suited to be optimized. They can spearhead revolutionary applications of mathematical optimization methods in industry and society (FN:M. Grötschel , R. Borndörfer, 2014. Mathematik im Verkehr. Heureka ‘14. FGSV Köln. ).
MATHEMATICS IN PUBLIC TRANSIT
Optimization and public transit fit well together. The rotations of buses and subways, and the schedules of their crews are nowadays commonly computed by optimization algorithms. Vehicle and crew scheduling lead to classical combinatorial optimization problems on network flows and path covers that are nowadays well understood. A solid theory and powerful algorithms have led to the development of mathematical vehicle and crew “optimizers”. These are on a mature level and available within the leading software systems for public transit companies (FN:R. Borndörfer, M. Grötschel, U. Jäger, 2010. Planning Problems in Public Transit. In Grötschel, Lucas, Mehrmann, EDS. Production Factor Mathematics. Acatech/Springer, p. 95-122.).
SUCCESS STORIES IN VEHICLESCHEDULING
Vehicle scheduling is about the “flow” of multiple types or “commodities” of vehicles through a graph of timetabled and deadhead trips (see Fig. 1). In Berlin, e.g., more than 1,000 buses of 50+ types serve more than 28,000 timetabled trips a day, connected by 100 million possible deadhead trips. Algorithmic techniques such as Lagrangean pricing, developed at ZIB, can identify the relevant parts of such gigantic graphs, and solve such problems to proven fleet optimality. Our BVG results still mark a world record in this area. The system-wide view allowed for shifts of vehicles between the morning peaks in the Eastern and Western parts of the city, resulting in substantial savings.
COMBINING ALGORITHMS FOR INTEGRATED PLANNING
Similar, but more complex methods, are used to schedule crews, producing a process chain, in which vehicles are scheduled first and crews second. Of course, doing both steps at the same time would be even better, and this type of integrated scheduling is a very active research topic.ZIB has pioneered this area by developing a bundle method, that allows the integrated optimization of vehicle and crew schedules for regional scenarios. This approach is based on a Lagrangean relaxation of the problem, which assumes that the two parts of the problem can also be addressed independently. This is sometimes a problem, for example in staff rostering, where it is hard to come up with a crew roster for a month if one has no idea about the daily duties. We have recently shown that Bender’s decomposition approaches can work in such a setting. Integrated optimizers based on Lagrange and Bender’s approaches will be the next level of optimization in public transit optimization.
WHY NOT OPTIMIZE THE BIG DECISIONS?
All of these methods only deal with implementing a given service at minimum cost. The real potentials, however, lie in the optimization of the public transport system itself. The network and the line plan, the timetable, and the fares can be optimized in order to find a best compromise between quality and costs. These problems deal with passenger behavior and are mathematically difficult. ZIB has developed a theory of path connectivity in order to solve line planning problems with a dynamic passenger routing, including a novel method to deal with direct connections and transfers. This model has been used to compute the line plan that is in operation at ViP Potsdam, a real breakthrough in this area.
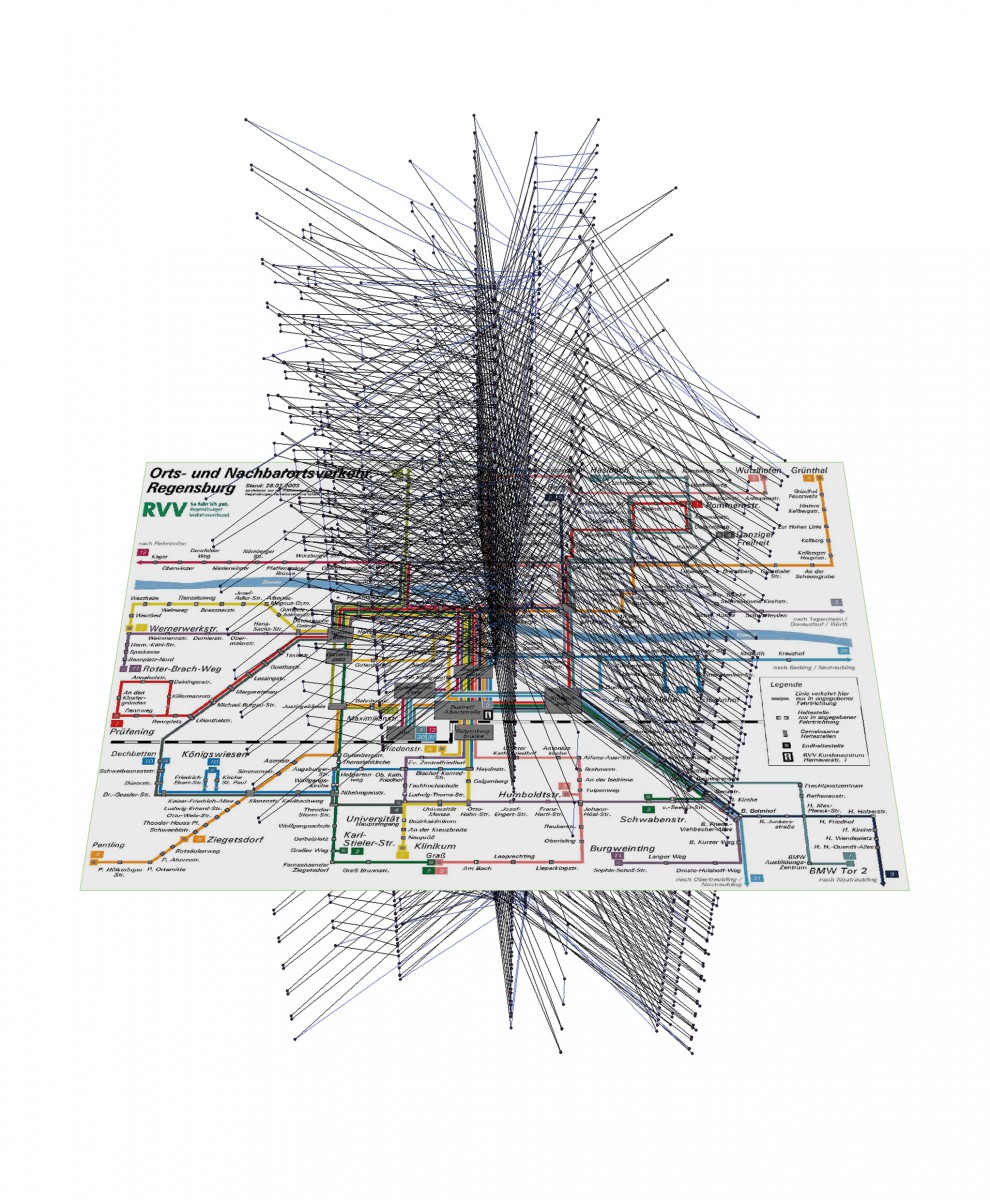
The typical star-shaped structure of an urban vehicle scheduling graph (only timetabled trips, time goes upwards).
RAILWAY OPTIMIZATION FINALLY WORKS
Railways are at the origins of traffic optimization, because trains must operate according to precisely planned schedules. Early works such as Tolstoí’s augmenting cycles, Ford and Fulkerson’s theory of network flows, and Charnes and Miller’s set partitioning approach were all invented for railway applications. These are, however, difficult: trains must keep safety distances, vehicles must be combined into trains, etc., i.e., railways require integrated planning approaches with an eye to many details.
WHY RAILWAYOPTIMIZATION IS SO DIFFICULT
Vehicle rotation planning (vehicle scheduling) must include train composition, and cannot be done on the level of individual vehicles, as in public transit. Extending bus rotation models by additional constraints did not work. In a project with DB Fernverkehr AG, we came up with a model that expresses transitions of vehicles in a train and the formation of trains from vehicles by configuration variables, that can be viewed as hyperarcs in a scheduling hypergraph, and consequently, vehicle rotations correspond to hyperflows. We have started to develop an algorithmic theory of hypergraphs that allows to solve, for the first time, large scale railway vehicle rotation planning problems for the entire ICE fleet of Deutsche Bahn on a strategic planning level. Now that the basic approach works, we can start to develop adaptive discretization techniques in order to address more detailed dated problems closer to the day of operation.
TRACK ALLOCATION
Once the rotations have been determined, train paths have to be embedded into the available network infrastructure. To this purpose, trains have to be assigned to particular tracks and platforms, and at precise times, such that minimum headways and other safety and technical constraints are satisfied. This so-called track allocation problem is also useful to determine infrastructure capacities in investment planning, or in a marketing process that allocates capacities according to the highest bid (this is actually prescribed in the German railway legislation). The track allocation problem is notoriously difficult. ZIB has developed a novel approach that is based on the consideration of train configurations on railway track segments using a bundle approach. With this technique, it was possible to solve, for the first time, instances involving several hundred infrastructure elements and several hundred trains. We used this method in project with the Swiss railways SBB in order to analyze the capacity of the Simplon corridor through the Alps under different regimes of operation (FN:R. Borndörfer, B. Erol, T. Graffagnino, T. Schlechte, E. Swarat 2010. Optimizing the Simplon Railway Corridor. Annals of OR.)
Railway optimization has finally started to work. Enormous potentials wait to be uncovered. These can substantially increase the overall attractivity of the railway system.

ICE high speed trains can consist of several railcars in different orders and orientations.
AIR TRAFFIC OPTIMIZATION FLIES
The airline industry started to boom in the eighties. Networks were reorganized in a hub-and-spoke fashion, new low cost carriers emerged, and prices fell, sometimes to unbelievably low levels. Many of these changes are closely linked to progress in mathematical optimization. Ticket prices are the result of sophisticated demand forecasts and revenue maximization methods that try to segment the market and skim the customers’ willingness to pay. Efficiency increases are due to fleet, aircraft rotation, and crew scheduling, they were first applied here at an industrial level. Today, all planning processes in the airline industry are heavily supported by mathematical optimization methods.
FAILURE SAFE PLANNING
In fact, efficiency has been pushed to a level that has eliminated many traditional buffers. In such a system, disruptions and delays can spread easily and it can happen that a plan that looked perfect on paper turns out to be very bad under only slightly unfavorable conditions. The consequence is to optimize not only under ideal conditions, but to anticipate possible failure situations. There are various concepts how to do that, ranging from stochastic optimization, which assumes complete knowledge of the probabilities of all possible failures, via a safeguarding against a worst case in robust optimization to online optimization without knowledge about the future. Failure safe planning is of course much more difficult from an algorithmic point of view, and it is not only a purely mathematical question to find the right concept.
MAKING AIRCRAFT ROTATIONS ROBUST
Computing robust rotations that can absorb delays up to a certain point by judiciously allocated buffer times is one question of this type. We have proposed a stochastic optimization concept that is based on propagating delays along individual aircraft rotations by an efficient computation of delay convolutions. It turned out that delays depend on relatively few factors, such that the associated probabilistic delay model can be used for forecasts. In simulations, reductions in expected propagated delays of up to 10% could be demonstrated (FN:R. Borndörfer, I. Dovica, I. Nowak, T. Schickinger 2010. Robust tail assignment. ZIB Report 10-08.).
FUEL EFFICIENT AIRCRAFT TRAJECTORIES
Air traffic has nowadays also reached a density where the airspace becomes crowded. Air traffic control reacts by enforcing more and more traffic restrictions. Their complexity has reached a level at which traditional optimization methods for aircraft trajectories are at their limits, and the increasing ranges of modern aircrafts don’t make the task easier, see Fig. 1 . New methods are needed in order to compute fuel efficient trajectories subject to changing weather conditions and complex air traffic restrictions. We investigate this problem in a new project with Lufthansa Systems Berlin, the manufacturer of the market leading LIDO software system for aircraft trajectory optimization.
INDIVIDUAL TRAFFIC
Car traffic is much more “anarchistic” than public transit. Rail and air traffic require optimization by a central powerful agency. Car traffic is more like a game, in which players pursue their interests and finally arrive at some kind of equilibrium solution. In fact, if we get stuck in a traffic jam every morning, we will try alternative routes, until we cannot improve our travel times any more. If we want to optimize car traffic, we must therefore take user behavior into account. This is, of course, difficult to predict. On the other hand, it is even more difficult to come up with a good system by trial and error, or by relying on some kind of evolution.
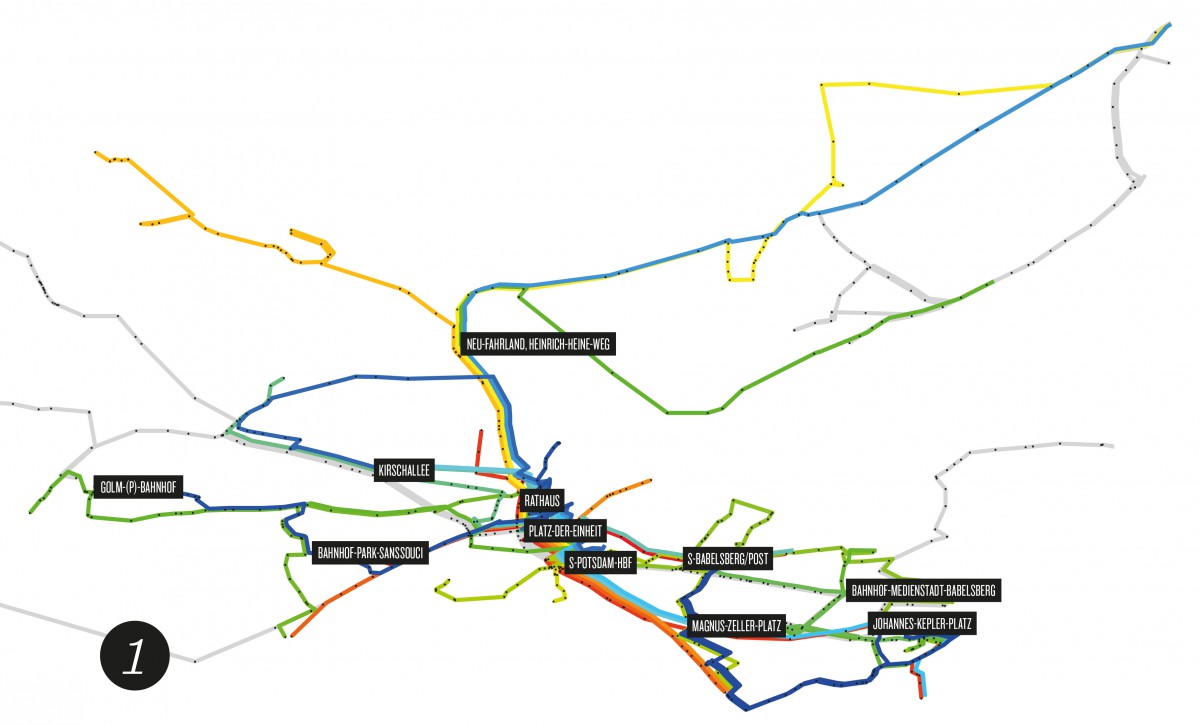
The public transport line system in Potsdam has been optimized for a best possible compromise between cost and quality of service.
INSPECTORS AGAINST FARE EVADERS
Highway fees are an example of an instrument that can be used to control individual traffic, in this case, truck traffic. In Germany, all trucks with a weight of at least 3.5 tons have to pay a highway fee depending mainly on the distance travelled and the vehicle weight. The toll is enforced by automatic gantry bridges and by highway inspectors, which perform mobile controls. In this case, the game is how to allocate the mobile controls in such a way as to establish a maximal level of control. In a project with the Bundesamt für Güterverkehr, which carries out these controls, we have developed a game theoretic approach to this problem, that predicts the behavior of fare evaders and plays a stochastic maximum control strategy against them. Moreover, the strategy can even be published without losing its efficiency. Such a strategy is way more effective than controlling, e.g., by the level of usage (FN:R. Borndörfer, G. Sagnol, E. Swarat 2011. An IP Approach to Toll Enforcement Optimization on German Motorways. OR 2011 Proceedings.) .
OPTIMIZING TRANSPORTATION SYSTEMS
Mathematical optimization has just started to unveil its enormous potentials in traffic and transport optimization. These are needed in order to solve the gigantic transportation problems of the present and future. Mathematics currently contributes most to operational planning problems to allocate and schedule vehicles and crews. This is important, but has a much smaller leverage than the big decisions of system design, see Fig. 1. It is not a good idea to pour the concrete first and think about an optimal operation of the resulting system afterwards. More effort must be invested into good planning, and mathematics is the key technology that makes the difference. This certainly also needs substantial mathematical progress. The start has been made, and the perspective is there: Mathematics can revolutionize traffic and transport.
