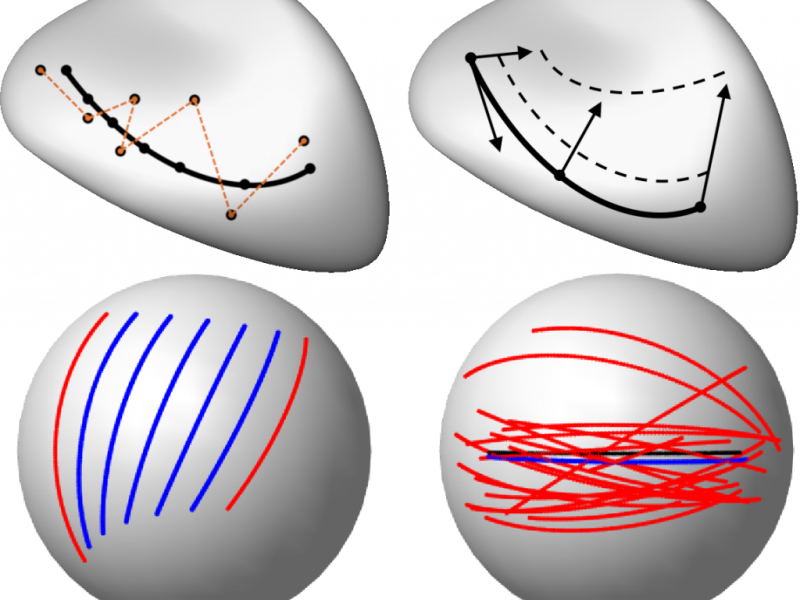
This project deals with spaces of manifold-valued curves and associated shape spaces, and is based on Riemannian tools for elastic shape analysis. We plan to study certain geometrically and physically motivated subspaces and to develop and apply a variational discrete-time framework for numerically solving the optimal correspondence problem and for consistently computing fundamental building blocks of Riemannian geometry. These include parallel transport, shortest paths as well as exponential and logarithmic mappings for these spaces. A desirable goal in many applications is to perform statistical analysis on the underlying infinite dimensional spaces, e.g., to capture the variability of trajectories and characterize their role in a large complex system, compute the mean, and perform classification or principal component analysis. For these purposes, we aim to develop robust and efficient schemes for approximation and interpolation of unparameterized curves and, in particular, a novel spline approach for data-driven modeling and longitudinal statistical analysis. Moreover, we extend some Euclidean results to general Riemannian manifolds. Much of the work will be devoted to applying the proposed approach to datasets from the broad areas of computer vision and morphology, including examples from epidemiology and molecular biology. The work will focus on intrinsic and constructive approaches and implement them as open source software.