Digital twins of real-world civil engineering structures such as bridges combine monitoring data and continuously updated simulation models. Their predictive capability supports informed decision-making on monitoring and maintenance. Simulation models are essential for estimating key performance indicators of bridges, such as load bearing capacity, durability, or safety. However, the underlying modeling assumptions may be wrong or insufficient for accurately reflecting reality.
In addition to the aleatoric uncertainty due to measurement noise and loads, the epistemic uncertainty of unknown parameters on one hand and of model deficiencies on the other hand affect the reliability of simulation predictions. While parameter estimation is well studied, detection and quantification of model deficiency is much less understood. This project aims at developing automated procedures for identifying model deficiencies and supporting the modeler in model improvement.
At Zuse Institute Berlin, the focus is on establishing reliable and efficient procedures for parameter identification: the problem is formulated in a Bayesian framework and Machine Learning techniques are adopted to reduce costs. Specifically, Gaussian Process Regression surrogate models are considered due to their stochastic nature.

Figure 1: FE model of a bridge (picture supplied by BAM)
Model set up
Given a PDE model, the Finite Elements techinque is considered. Three main sources of model discrepancy are introduced at this level:
- constitutive equations not adequate or not considering some factors;
- boundary conditions and the modelling of the connection of different model parts;
- discretization error.
The latter error term is controlled through mesh refinement: the FE discretization is not fixed but can be refined, providing a better numerical approximation for greater computational work.
Bayesian inverse problem
A Bayesian perspective is adopted to identify unknown parameters. Since an inverse problem requires multiple model evaluations and the FE model is costly to evaluate, a surrogate model is introduced. Different relations between the surrogate and the FE model result in different inverse problems and, consequently, different posterior distributions.
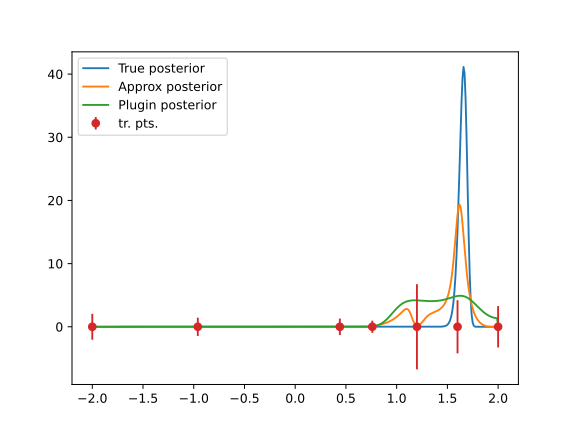
Figure 2: true posterior and two different approximations on 1D parameter space.
Once the problem is formulated, classical statistical techniques are considered to reconstruct parameters:
- Sequential Monte Carlo and other Markov Chain Monte Carlo (MCMC) techniques.
- For a posterior distribution of high dimension, a variational Bayesian approach is considered.
Adaptive Gaussian Process Regression for posterior sampling
The training set for the GP is built in a posterior-oriented fashion: we minimize the error on the posterior distribution under a computational budget constraint. Since the impact that design choices have on the error quantity is not known a priori, we follow a sequential greedy approach. The computational cost is approximated by asymptotical estimates.
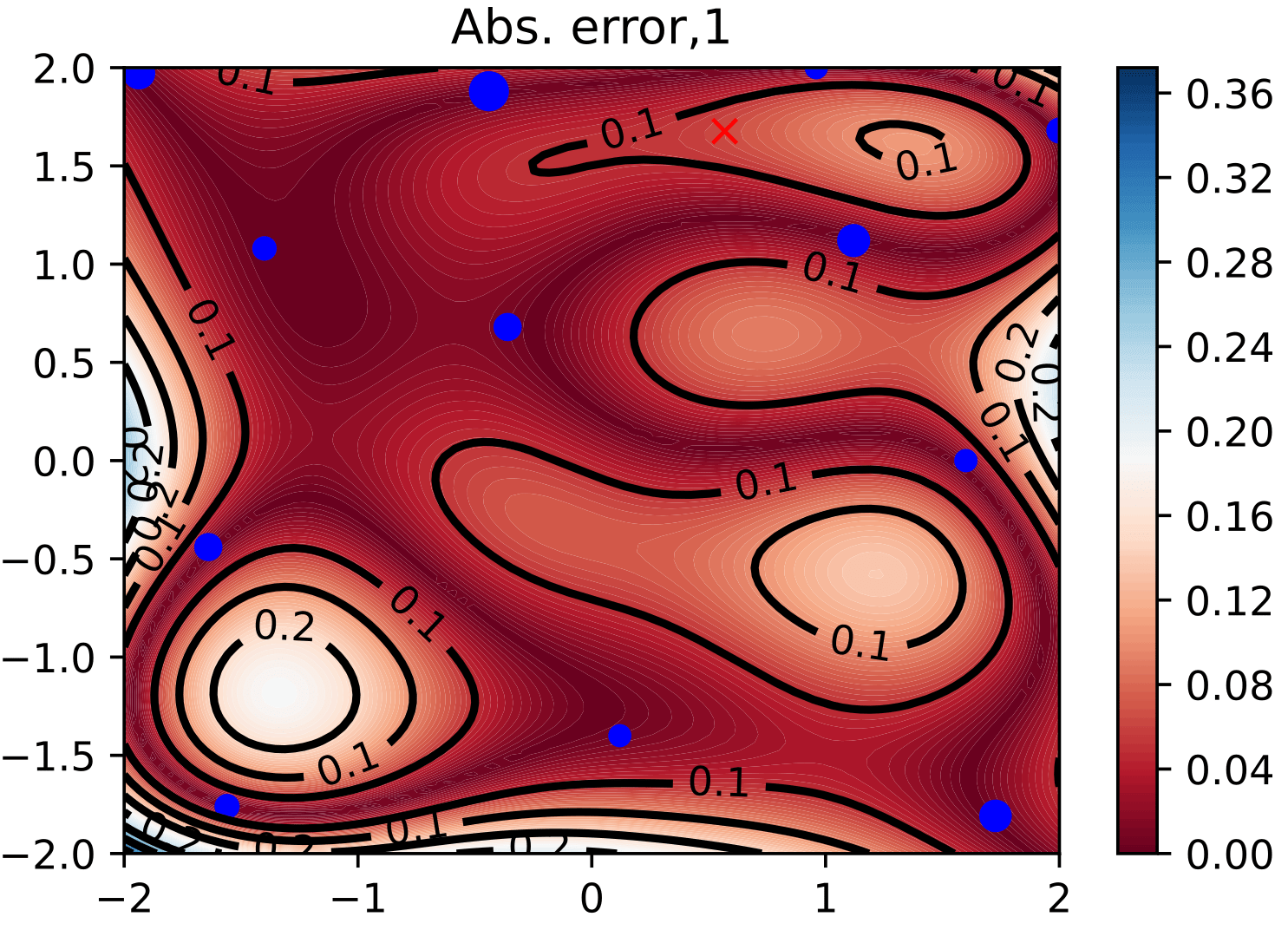
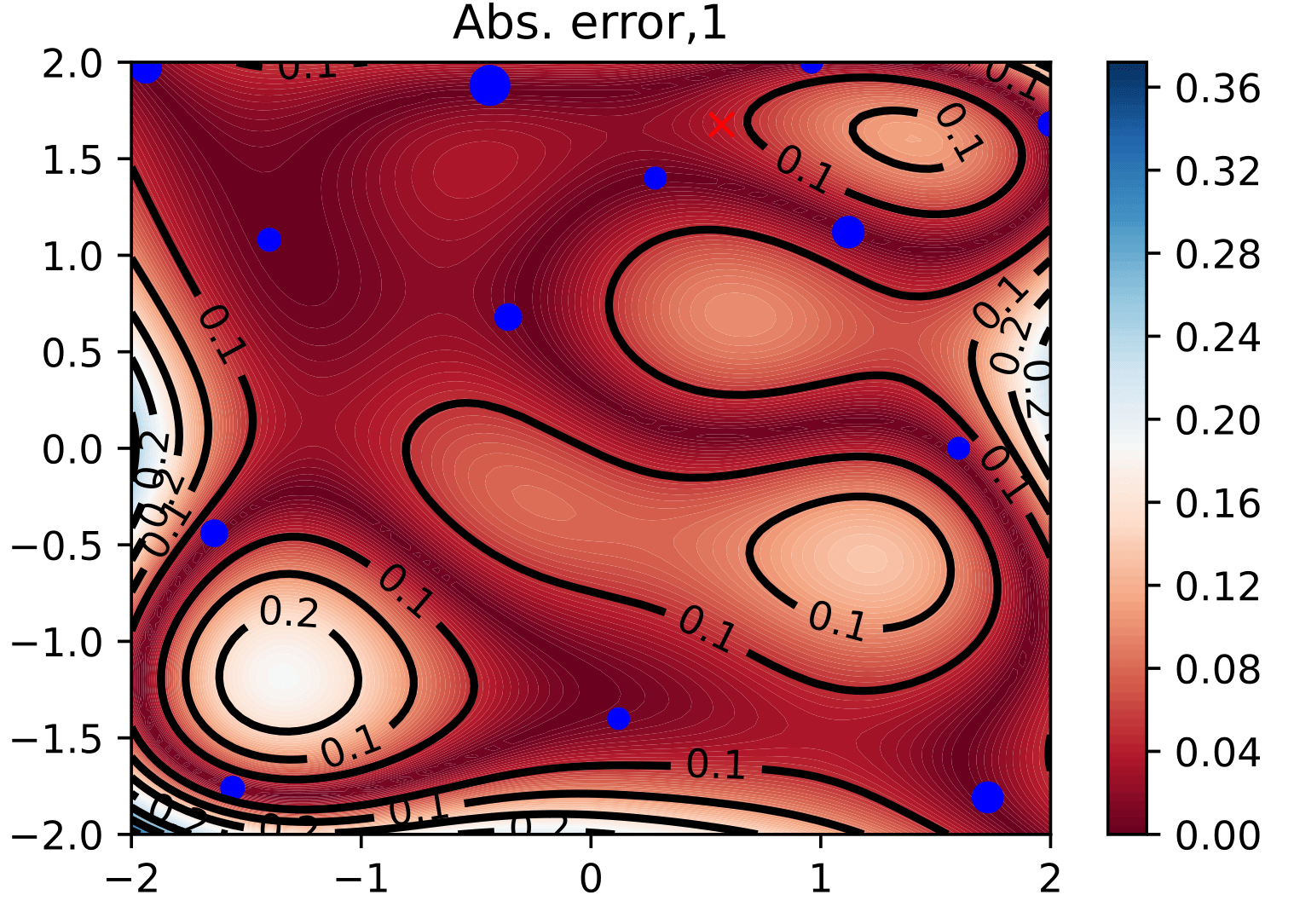
Figure 3: reduction of model error with adaptive sampling on 2D parameter space. The error is reduced in those areas where the posterior places significant mass.
Model bias
Even a well fitted model will not be able to describe perfectly reality. We investigate strategies to improve the model and identify its bias. We consider:
- non parametric GP bias added to the output or to the constitutive equations, respectively
- mixture models admitting two or more sets of parameters for providing insights on the dependency of optimal parameters on other quantities
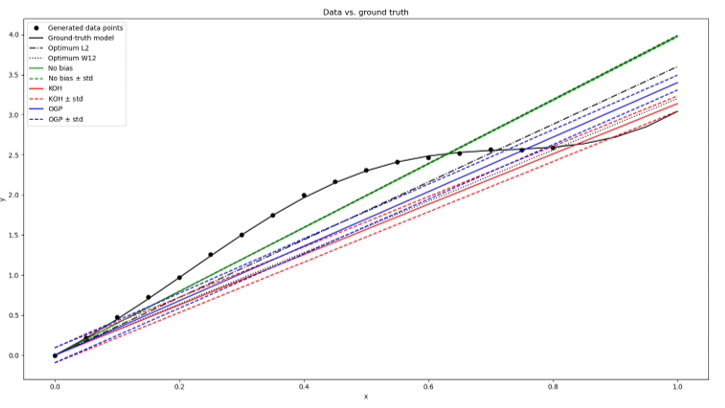
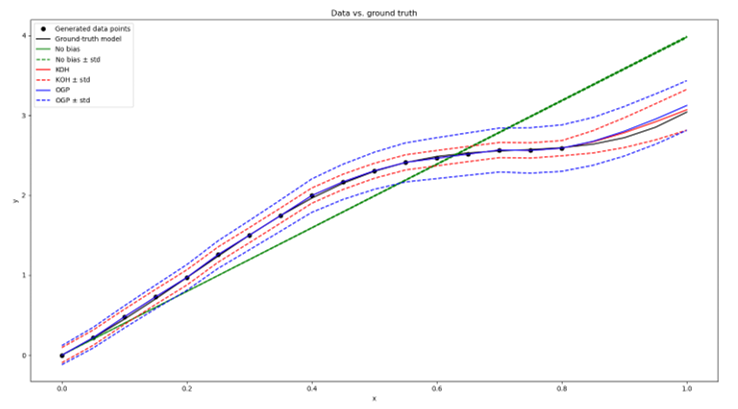
Figure 4: Model bias approaches for linear regression (pictures supplied by BAM)
