Transportation networks are a daily encounter for us all. Maintaining smooth operations is a paramount objective both for quality of service and public finances. For the S-Bahn Berlin, optimizing periodic timetables is a complex challenge, especially due to turning constraints that arise at terminals and stations. Addressing these issues is crucial for preventing conflicts and ensuring reliable service. Our project tackles this problem by employing geometry-inspired duality approaches, integrating advanced mathematical techniques such as mixed-integer programming, Benders decomposition, matroids, hyperplane arrangements, and zonotopes. The aim of these innovations is to create robust and efficient timetables to enable better performance.
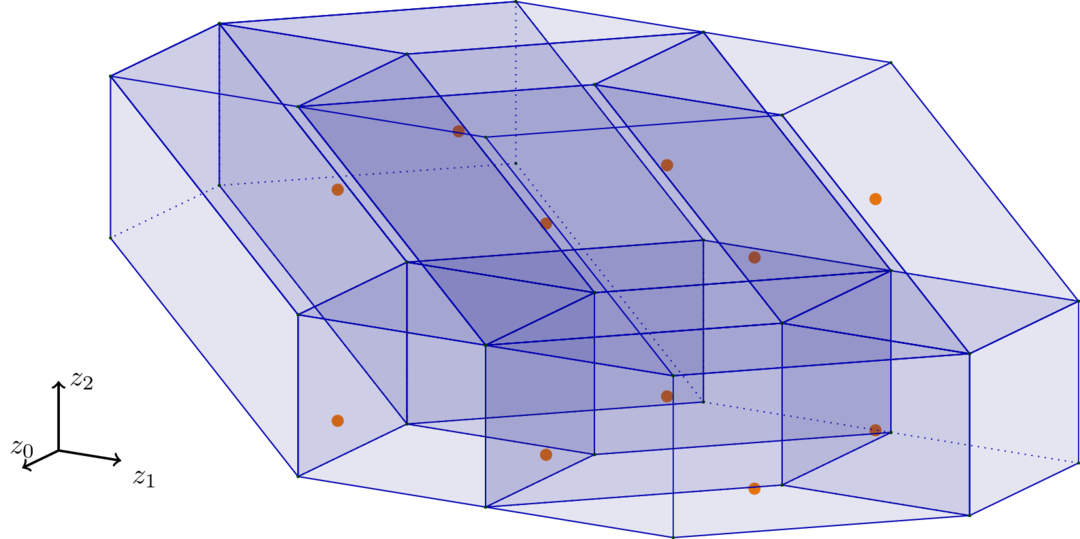
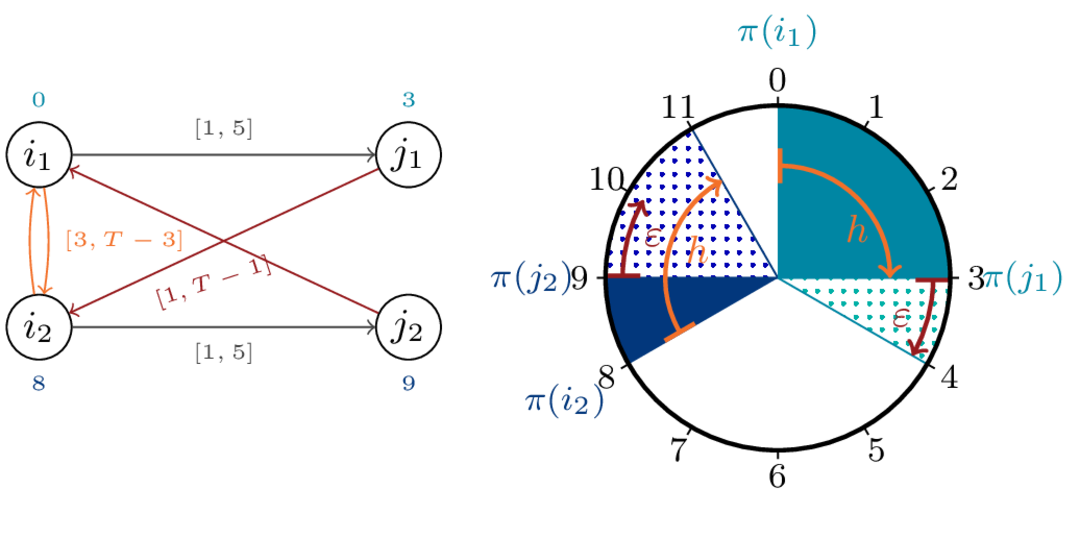
We focus on timetable optimization, particularly on the Periodic Event Scheduling Problem (PESP), the cornerstone of periodic timetable optimization. Its geomtry is of special interest, showcasing an interesting duality in its variables, linking polytropes and zonotopes. These properties were recently used to devise novel solving heuristics, and we intend to keep working on this line. Our primary tool are mixed-integer linear programs, to extend PESP and integrate various constraints of practical interest. Within them, geometric insight drives the nature of our models, allowing for novel and more effective use of cutting planes, such as with cyclic order constraints.
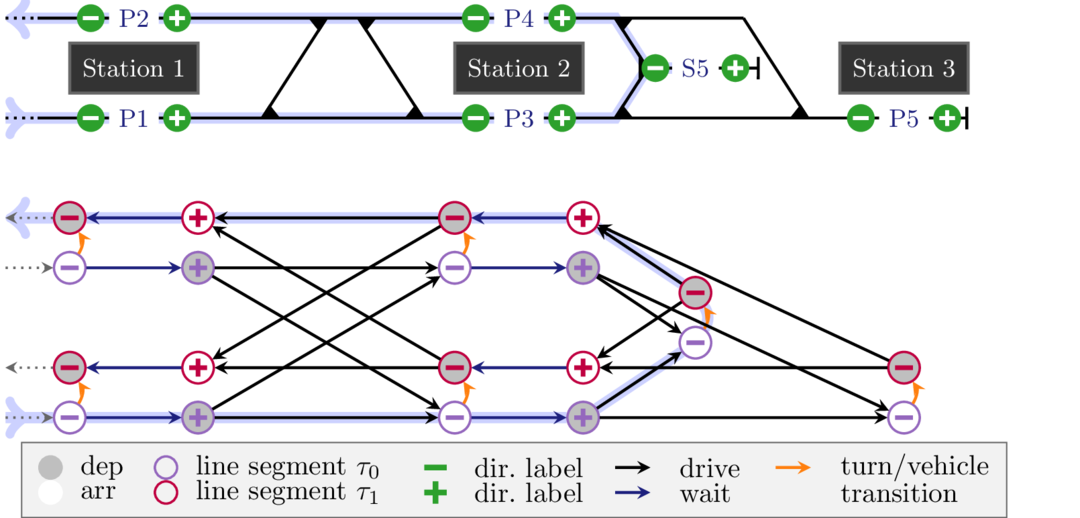
This project canvasses periodic timetabling, discrete geometry, and railway operations practice, leveraging interdisciplinary experience to develop innovative solutions for the S-Bahn Berlin network. By bridging these fields, we provide advanced theoretical understanding of periodic timetabling in general, but also comprehensive strategies to be implemented in real-world scenarios, ultimately enhancing the efficiency and reliability of the S-Bahn Berlin network.
The project is funded by the Berlin Mathematics Research Center MATH+ and belongs to the MATH+ Partnership Area PaA-3.
