Towards understanding the organizational principles of life
Biological processes involve different dimensional scales in space and time, ranging from molecular interactions to cellular signaling, cell-cell interactions, tissue formation, and systemic regulation, for example by hormones. These dynamic processes are highly interrelated such that the system behavior can usually not be predicted solely from the behavior of its individual components. A systems approach is needed in terms of a quantitative analysis of these dynamic networks and structures by computational modeling. At ZIB we aim at understanding biological and biochemical processes with a high spatio-temporal resolution by extracting biological structures from large-scale microscopy and by mathematical modelling of biological networks.
Fluorescence image of a neuronal culture created by stitching together six images collected at 40x magnification. Honorable Mention, 2011 Olympus BioScapes Digital Imaging Competition®.
A VIRTUAL HOSPITAL FOR REPRODUCTIVE MEDICINE
For many couples, having children is one of the major aims of life. Failure is associated with guilt, inadequacy, and loss of the sense of purpose in life, bearing an increased risk for negative psycho-social functioning. Furthermore, changes in population demographics and greater focus on education and careers among women have resulted in greater numbers of women attempting pregnancy at more advanced ages when they are inherently less biologically fertile. In Europe, for example, infertility affects 10% to 15% of couples at the reproductive age.
Human fertility is based on physiological events like adequate follicle maturation, ovulation, ovum fertilization, corpus luteum formation, as well as endometrial implantation, proceeding in a chronological order. Diseases such as endometriosis or polycystic ovary syndrome seriously disturb menstrual cycle patterns, oocyte maturation, and, consequently, fertility. Besides endocrine diseases, several environmental and lifestyle factors, especially smoking and obesity, also have a negative impact on fertility.
Modern assisted reproductive technologies have dramatically increased the chances for successful pregnancy. Nevertheless, current success rates have only reached 35%, even in leading clinical centers. The main reason is a limited understanding of the large inter- and intra-individual variability in hormonal regulation. We tackle this problem within the collaborative research project PAEON – Model Driven Computation of Treatments for Infertility Related Endocrinological Diseases, which has been funded by the European Commission since 2013. Partners of the Computational Systems Biology group at ZIB are the Sapienza University of Rome, the Lucerne University of Applied Sciences and Art, the Hannover Medical School, and the University Hospital Zurich.
Within this project the problem is addressed with a systems biology approach that aims at integrating clinical data with mathematical modeling of the complex biological system (FN:S. Röblitz, C. Stötzel, P. Deuflhard, H. M. Jones, D.-O. Azulay, P. van der Graaf, S. W. Martin. A mathematical model of the human menstrual cycle for the administration of GnRH analogues, Journal of Theoretical Biology. 321:8–27, 2013.). Although the relevant components and feedback mechanisms have been identified from experiments and have been described qualitatively for many years, dynamic mathematical models for the periodic changes in hormone levels and follicular function started being developed only a few years ago. From a mathematical point of view, the challenge is to represent a single real patient or a patient population with virtual patients, whereby a virtual patient is characterized by a specific parametrization of the model equations (FN:T. Mancini, I. Salvo, F. Mari, I. Melatti, A. Massini, S. Sinisi, E. Trondi, F. Davi, T. Dierkes, R. Ehrig, S. Röblitz, B. Leeners, T. Krüger, M. Egli, F. Ille. Patient-Specific Models from Inter-Patient Biological Models and Clinical Records, Formal Methods in Computer-Aided Design. 2014.). For this purpose, statistical model checking and Bayesian methods for parameter inference are applied.
The goal of the mathematical approach is to develop a model-based clinical decision support system for physicians (FN:R. Ehrig, T. Dierkes, S. Schäfer, S. Röblitz, E. Tronci, T. Mancini, I. Salvo, V. Alimguzhin, F. Mari, I. Melatti, A. Massini, T. H. C. Krüger, M. Egli, F. Ille, B. Leeners. An integrative approach for model driven computation of treatments in reproductive medicine, In: BIOMAT - Proceedings of the 15th International Symposium on Mathematical and Computational Biology, Rorkee, India, 2015.). As part of a software called “virtual hospital,” such a system contributes to a better understanding of the highly complex processes in the female cycle and provides the opportunity to simulate and optimize treatment strategies on the computer, thus finding patient-specific treatments with the highest expected success rates.
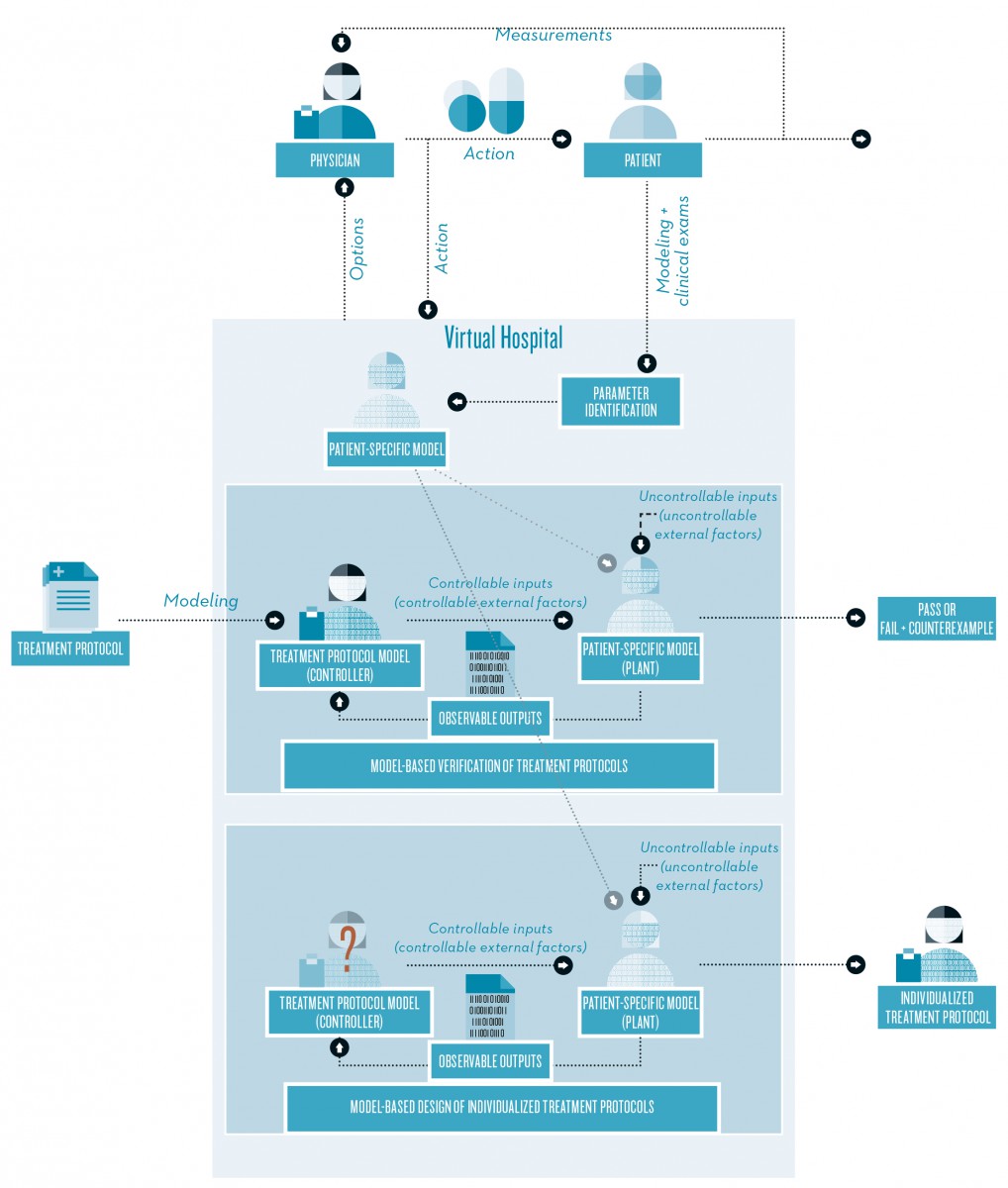
In the virtual hospital a physician enters real patient data into the system and proposes an action, a specific treatment strategy, for example. The system then predicts a patient-specific success rate for the proposed treatment (model-based verification of treatment protocols) or even proposes a modified treatment with a higher expected success rate (model-based design of individualized treatment protocols). The output contains options to be performed on the patient, like dosing recommendations or days where measurements should be taken. Note that the output is just a recommendation, the final decision is made by the physician.
HIGH-PERFORMANCE DAIRY COWS – A METABOLIC CHALLENGE
Modern dairy cows produce up to 50 litres of milk per day. This is an enormous challenge for the organism that needs to provide the substrates and the energy. Therefore, high-producing dairy cows often suffer from prevalent diseases which affect their metabolism and, as a consequence, lead to reduced fertility. Over the last few decades, animal scientists have studied the complex interplay between energy balance, nutrition, milk yield, and fertility, and collected large amounts of data, in vitro as well as in vivo. In order to find and understand the biological mechanisms that arise from the dynamic interactions of the different components, a systems biology approach is needed to analyze and integrate these data into predictive mathematical models in silico.
We are facing this challenge within the Junior Research Group project BovSys, which is funded for five years by the Federal Ministry of Education and Research (BMBF). Our aim is the development of a dynamic, mechanistic, mathematical model of genetic, nutritional, and physiological control of reproductive processes in dairy cattle. Integrated into larger models and software for herd or farm management, this research contributes to a sustainable production of food and a predictive veterinary practice, including an early warning for disease and the identification of new targets for diagnosis and treatment.
Currently, we are working with two major models of physiological networks that are related to the hormonal regulation, energy, and mineral metabolism of dairy cows: a model for the bovine estrous cycle (FN:C. Stötzel, R. Ehrig, H. Marike T. Boer, J. Plöntzke, S. Röblitz. Exploration of different wave patterns in a model of the bovine estrous cycle by Fourier analysis. BIOMAT – Proceedings of the 14th International Symposium on Mathematical and Computational Biology, 2015.), named BovCycle, and a model for potassium balance (FN:. Plöntzke, M. Berg, A. Olany, S. Leonhard-Marek, K. E. Müller, S. Röblitz. Modelling potassium balance in dairy cows, ZIB-Report 13-09, 2013.). Both models are linked by a model for the glucose-insulin interaction (FN:J. Plöntzke, M. Berg, C. Stötzel, S. Röblitz: A systems biology approach to bovine fertility and metabolism: Development of a glucose insulin model. ZIB-Report 15-51, 2015.) that is known to influence both networks. There are pharmaceutical interventions frequently performed in veterinary practice, like application of glucocorticoids, whose effects on potassium balance and reproduction have not yet been studied in detail. We are particularly interested in conducting in-silico simulations of such interventions. Studying the systems’ behavior gives new insights into short- and long-term effects and interactions of drug administrations, without the need for new animal experiments.
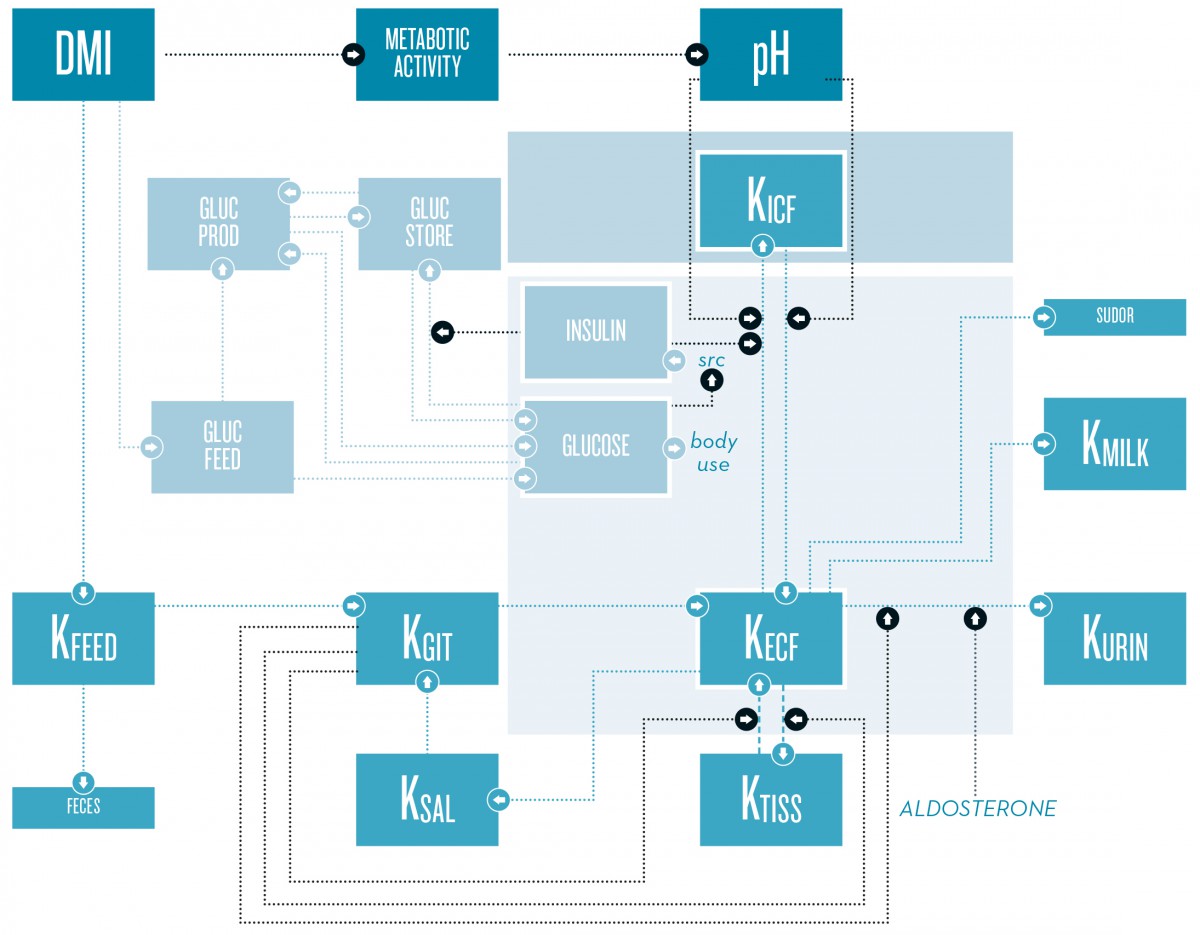
Potassium balance in dairy cows is the result of dry matter intake (DMI), distribution inside the organism, and excretion, mainly via urine, milk, feces, and sudor. Distribution between the extracellular fluid (ECF) and intracellular fluid (ICF) is influenced by the glucose-insulin metabolism and pH.
MICROSCOPY IMAGE ANALYSIS FOR UNDERSTANDING MOLECULAR SIGNALING
Many processes in systems biology depend on molecular signals. Such signals can control the behavior of cells. The signals can, for example, stimulate growth or cell migration. The effect of signal proteins is impor-tant for many processes in the human body. It is also crucial for understanding diseases like cancer. One of the main characteristics of cancer is an increased angiogenesis, the attraction of blood vessels. Tumors can emit signal proteins like Vascular Endothelial Growth Factor (VEGF) to attract the formation of new blood vessels towards it in order to grow even faster.
In collaboration with the Institute of Chemistry and Biochemistry at FU Berlin, we have been working on understanding molecular signaling in cells experimentally. We develop analysis methods and software that enable biologists to investigate cell behavior under various conditions. One example are factors that control cell migration, which can be identified using chemotaxis migration assays. Therefore, hundreds of epithelial cells from the human umbilical vein (HUVECs) are seeded in the middle of a two-chamber glass slide. In one condition, both chambers are filled with a nutrition-free medium. In a second condition, low doses of VEGF are added to the lower chamber. Cell migration is then monitored using a phase-contrast microscope, acquiring a sequence of images over 16 hours with a five-minute interval, in order to detect the preferred migration direction. To analyze and quantify the migration behavior objectively, we developed a method to track the movement of individual cells robustly. The exact position for around 500 cells for almost 200 time points alone, however, is not sufficient to understand the migration behavior, because cell migration is a complex biophysical process, and the migration appears chaotic at first glance. When a growth factor like VEGF is present, cells are only expected to have a preferred migration direction, although they do not migrate straight towards the growth factor.
In this example, we applied Markov State Models (MSM) to model, analyze, and visualize the relevant migration patterns. One of these analyses is the Committor Analysis, which calculates the probability for a cell to migrate to the lower image border before reaching the upper border.
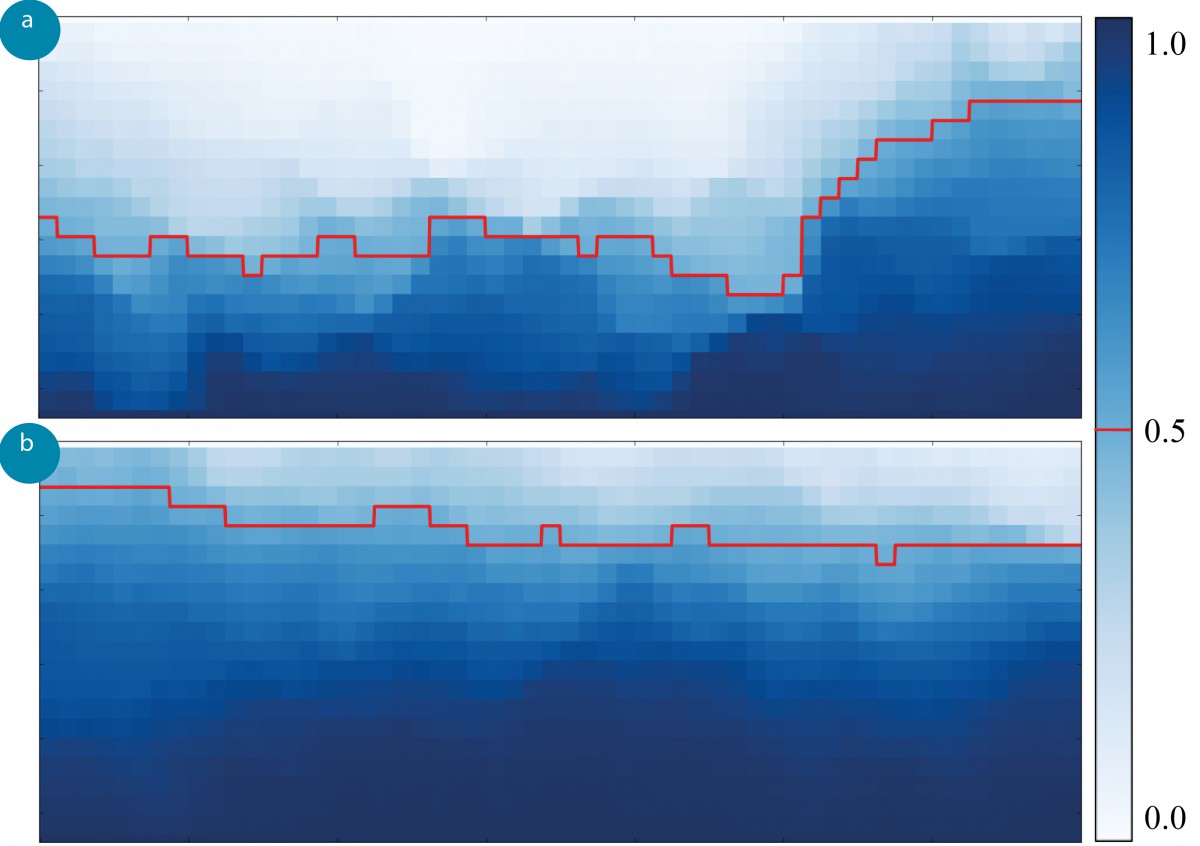
Results of the committor analysis. The color represents the probability for a cell to migrate towards the lower image border rather than the upper image border, and the 0.5 isoline indicates that all cells below are more likely to migrate downwards and vice versa. Figure a) above depicts the results from the experiment without a gradient. The isoline is located around the image center, thus cells will most likely migrate towards their nearest chamber. The results from the VEGF experiment are depicted in Figure b), where the isoline is clearly shifted upwards. This indicates that cells on most of the image area will probably migrate downwards, where the VEGF-filled chamber is located.

Cells are most likely to migrate towards their closest chamber when no growth factor is present A). But in the presence of VEGF in the lower chamber, most cells tend to migrate towards the VEGF B). Our analysis allows us to detect and quantify such effects.
DISCRETE OR CONTINUOUS – HOW TO DESCRIBE BIOLOGY with MATHEMATICAL EQUATIONS
Typical experiments on single cells or tissue involve measurements of gene expression levels or the identification and quantification of certain molecules, proteins, for example, as well as techniques for analysing the dynamics and interactions between the measured components. The systems biology approach aims at creating, refining, and retesting mechanistic, mathematical models to accurately reflect the experimental observations and to make predictions about the system’s behavior upon environmental changes.
The first step in that process is to decide on a suitable mathematical formalism. That means, the modeler has to decide if the state space of the model (activation levels, molecule numbers, or concentrations, for example), the time variable, and the space variable are discrete (integers) or continuous (real numbers), and if there are stochastic fluctuations present or not. This choice depends on the quality of the available measurements and on the research question to be answered. Examples of modeling formalisms include Boolean networks, ordinary differential equations (ODEs), and the chemical master equation (CME) for spatially homogeneous systems, or partial differential equations (PDEs) and the spatio-temporal master equation (STCME) for inhomogeneous systems. Boolean networks, for example, were introduced as qualitative models of genetic regulatory networks, where genes are modeled as binary switches, whereas ODEs and CMEs can be used to describe chemical reaction networks.
Every modeling approach has its advantages and disadvantages. Generally, fine-scaled models allow more detailed statements about a system, but are often costly to solve, and the uncertainty in the prediction is much higher because the number of unknown model parameters is usually very large. Our research focuses on the development of efficient algorithms for the numerical solution of such models (FN:I. Kryven, S. Röblitz, C. Schütte. Solution of the chemical master equation by radial basis functions approximation with interface tracking. BMC Systems Biology. 9:67, 2015.) as well as on the quantification of uncertainty in model predictions.
Coarse-grained models, on the other hand, are often easier to solve. They allow for a comprehensive analysis of the state and parameter space, but do not resolve all details of the underlying biological mechanisms. Common to all modeling formalisms is the fact that a model always constitutes a simplification of reality, focusing on particular aspects of interest and neglecting details either by design or simply due to a lack of knowledge.
Hence, our research at ZIB aims at combining different methods by using complementary modeling approaches and by building hybrid models. Utilizing different modeling approaches in parallel provides an alternative view on system characteristics and highlights modeling artifacts. For example, a complementary analysis of an ODE model for the bovine estrous cycle (FN:C. Stötzel, M. Apri, S. Röblitz. A reduced ODE model of the bovine estrous cycle. ZIB-report 14-33, 2014.) using a Boolean network led to new insights regarding the regulation among the components, and also indicated strongly that the system is tailored to generate stable oscillations (FN:C. Stötzel, S. Röblitz, H. Siebert. Complementing ODE-Based System Analysis Using Boolean Networks Derived from an Euler-Like Transformation. PloS ONE. 10(10): e0140954, 2015.). However, the mathematical questions of property conservation across formalisms, as well as the derivation of hybrid models in the presence of scaling cascades, are still largely unaddressed and will be in the focus of our future research.
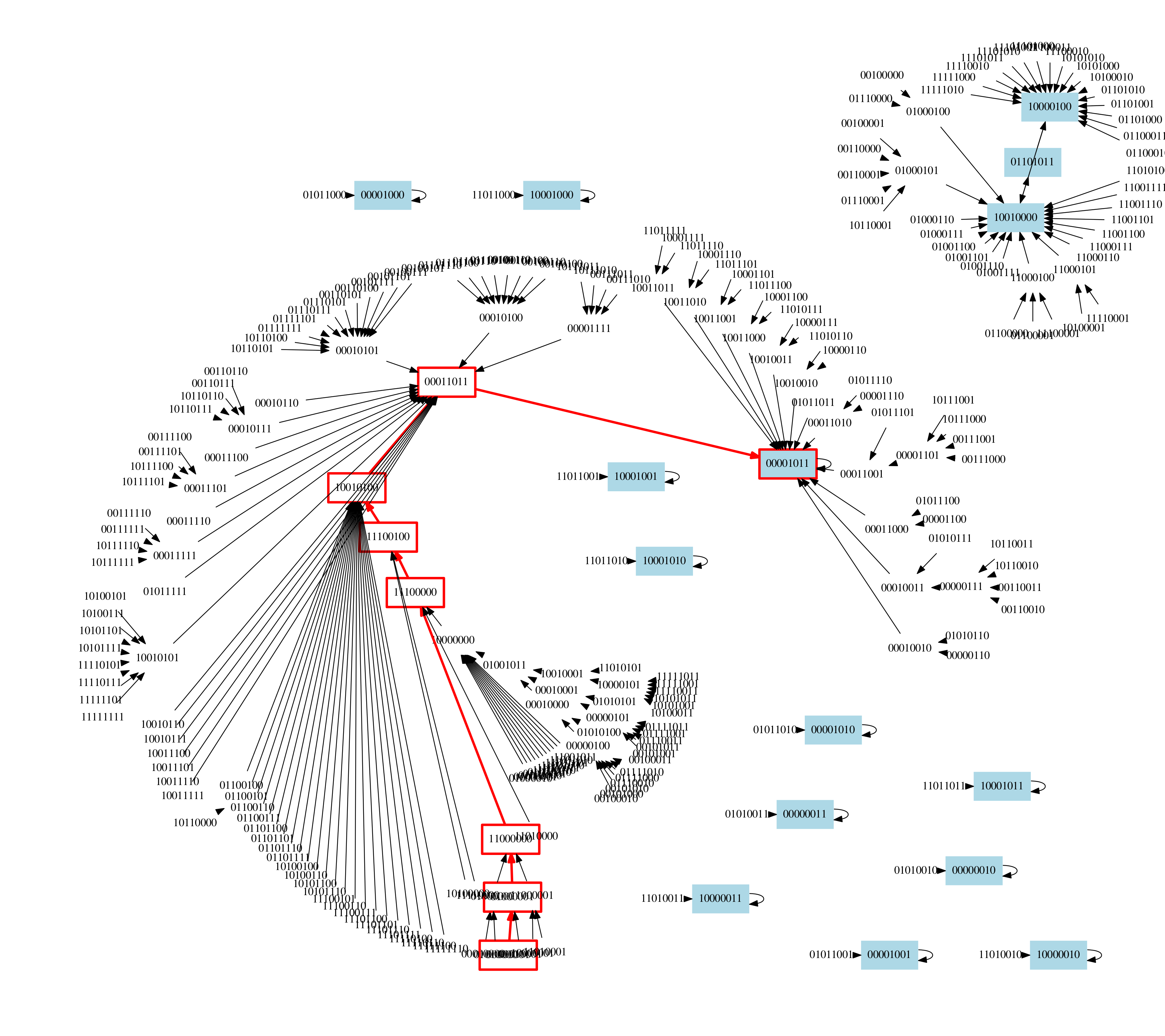
The state space and trajectories of a Boolean model of the cell cycle in fission yeast (M. Davidich, S. Bornholdt. Boolean Network Model Predicts Cell Cycle Sequence of Fission Yeast. PLOS ONE, 2008.). The red transitions represent the different phases of the cell cycle. In blue are other attractor states predicted by the model (Courtesy H. Klarner).
SYSTEMS BIOLOGY SOFTWARE DEVELOPED AT ZIB
Modeling, parameter identification, and simulation play an important role in systems biology (FN:P. Deuflhard, S. Röblitz. A Guide to Numerical Modelling in System Biology. Springer International Publishing, 2015.). Computational system biology without efficient numerical software is hardly imaginable. Biological systems, the female menstrual cycle or cellular signaling processes, for example, are as diverse as they are complex. All these different systems, translated into the mathematical language, can be investigated and analyzed by our software: interactive, simple to use, and, most importantly, easily extensible for novel approaches. Our software is suitable not only for innovative research, but also for day-to-day teaching purposes. The software development process is done completely openly, accessible to everyone, as is all of our software.
To date, we have developed the software packages BioPARKIN(FN:https://github.com/CSB-at-ZIB/BioPARKIN) and ZIB_RubyExt(FN:https://github.com/CSB-at-ZIB/ZIB_RubyExt), both publicly available at GitHub. Both packages involve long-standing mathematical codes for the numerical solution of ordinary differential equation systems, or simulation, and for parameter identification. In addition, they provide accurate and efficient numerical routines for solving the sensitivity equations; that is, for computing the sensitivity of the simulation results with respect to the model parameters. In our software, the effort for this computation only grows linearly with the number of model parameters, whereas the effort in standard implementations grows quadratically. Further speed-up in ZIB_RubyExt compared to BioPARKIN is obtained by making use of a library for automatic differentiation.
Both BioPARKIn and ZIB_RubyExt are compliant with the Systems Biology Markup Language (SBML), which has become the standard for representing models in systems biology. BioPARKIN consists of a computational core in C++ and a user-friendly graphical interface in Python, which hides the complicated math and makes it easy to use for non-mathematicians. Compared to BioPARKIN, ZIB_RubyExt is even more versatile, robust, and fast. ZIB_RubyExt makes use of numerical FORTRAN routines in Ruby. It is extremely easy to extend by the inheritance scheme of Ruby, similar to a plug-in mechanism. In addition, it is Web/mobile application ready, which paves the way for its use in clinical decision support systems or personal health records, for example.
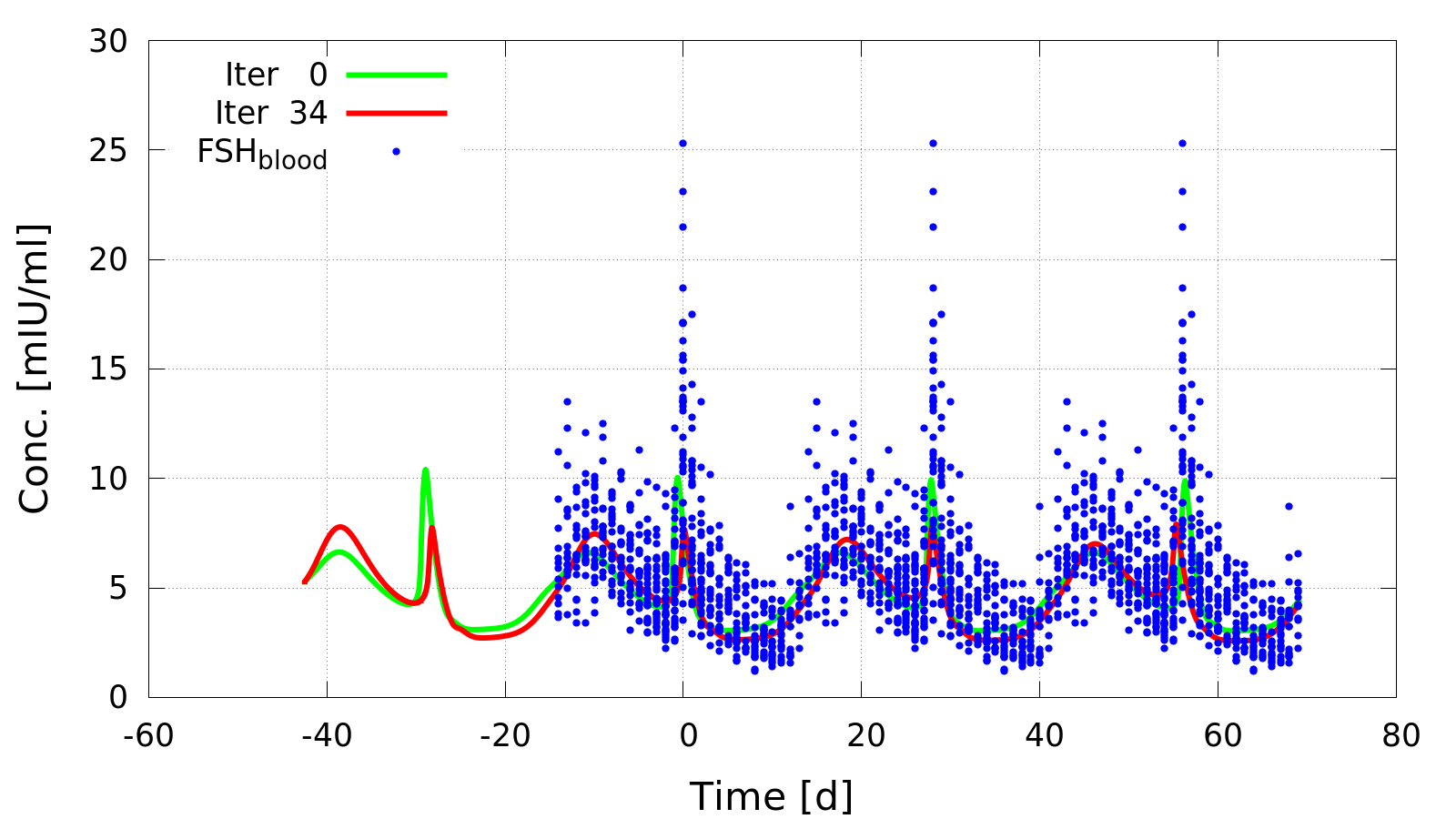
Parameter identification result obtained by Gauss-Newton iteration in ZIB_RubyExt. Parameters in a model of the human menstrual cycle were estimated such that simulation results (solid lines) fit to measurements of hormone blood concentrations, including the follicle stimulating hormone FSH (blue dots).