In this project, we concern ourselves with line plan optimization on a symmetric city model. We evaluate whether and how often asymmetric solutions can occur despite the entirely symmetric input. Further, we examine how much the costs of symmetric line plans deviate from the optimum and whether symmetric line plans can be used to approximate optimal solutions.
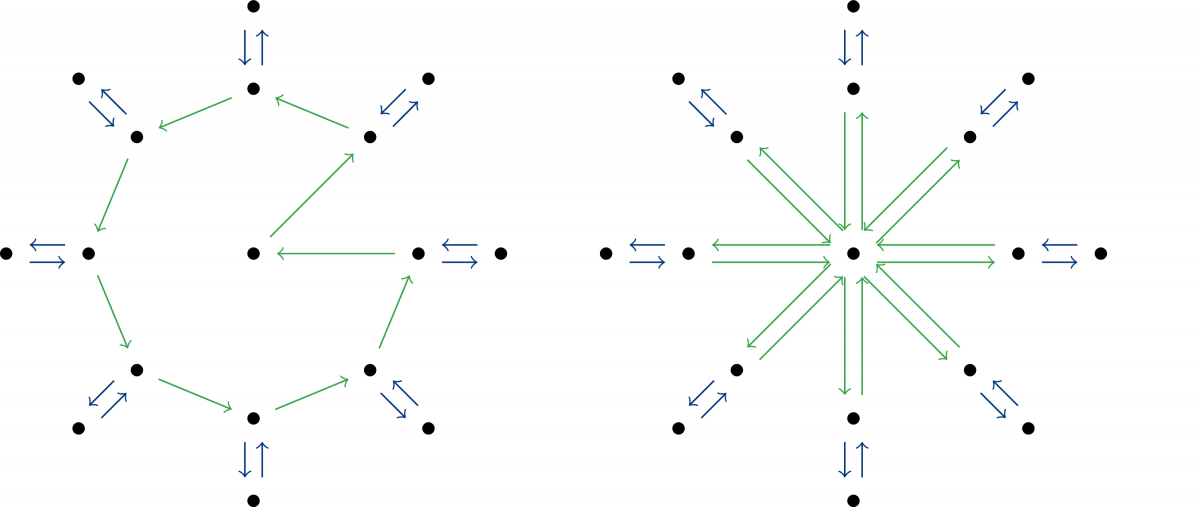
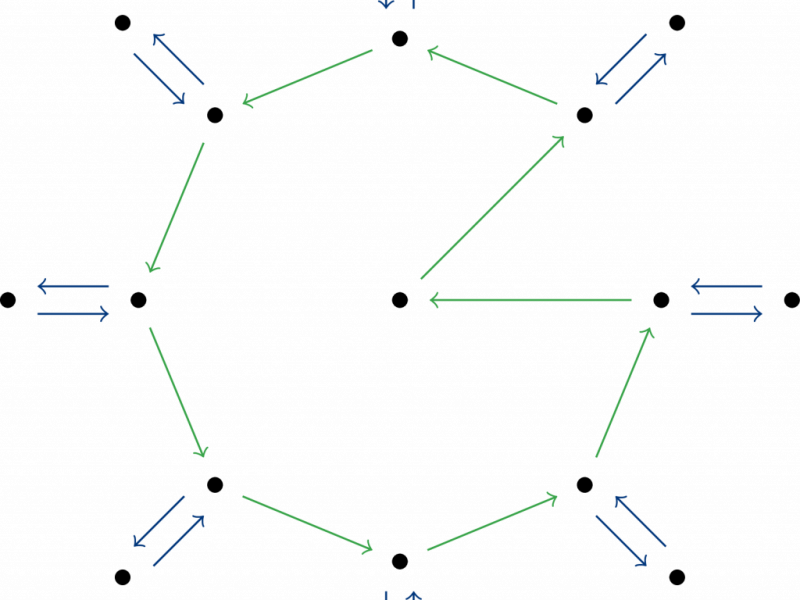
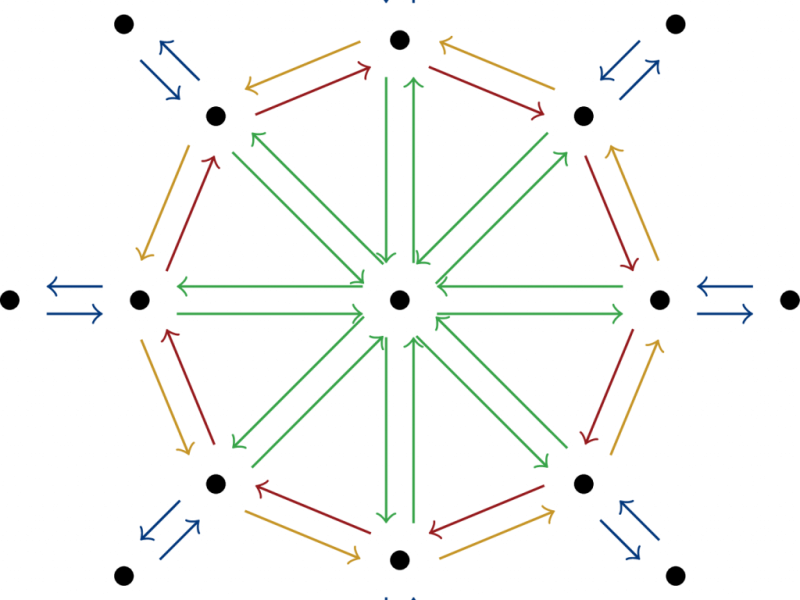
Line planning is one of the first steps in the optimization of public transportation services: It involves the determination of vehicle routes and needed frequencies in order to cover the travel demand in a city. Line planning is often performed on a graph which is a simplified and generalized city representation and usually displays a high degree of symmetry in both the geometry and demand. In a way, it is natural to assume that the best line plan is then symmetric as well -- one could be inclined to exploit this symmetry and obtain the best line plan for one zone only and extrapolate the line plan for the entire system as a symmetric copy of the one zone. However, this is not necessarily the case. We formulate the line planning problem with a mixed integer linear programming formulation and apply it to a generic model, the Parametric City. The latter was introduced by Fielbaum et al. to represent different city types and is, in particular, symmetric in both geometry and demand.
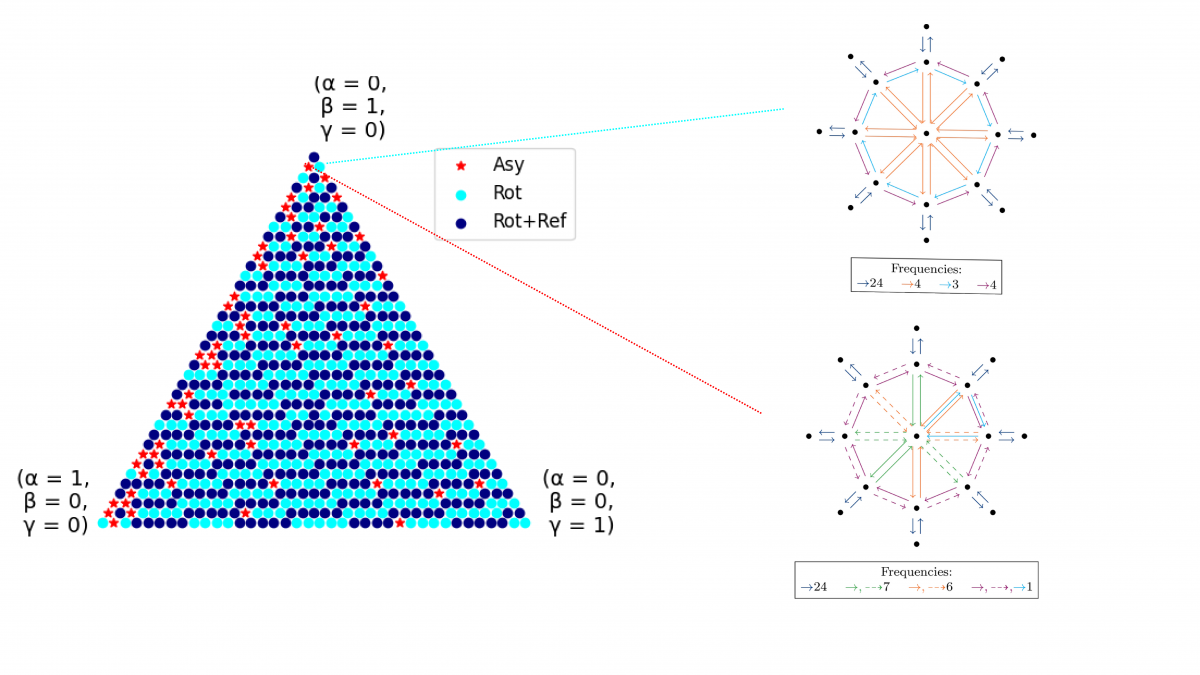
In this project, we concern ourselves with the influence of said symmetries: In which cases are the optimal line plans symmetric as well? When are symmetric line plans an especially bad choice? As symmetric line plans are easy to compute, can these be exploited to approximate optimal solutions in some cases?
We examine the problem with group theoretical means, inspect properties of symmetric solutions and introduce a symmetry gap to measure the deviation in costs of symmetric solutions to the optimum and determining bounds on said gap. This allows us to deduce an approximation algorithm for the line planning problem in the Parametric City. In special cases, however, line planners should take particular care, since the optimal solution has significantly lower costs than the symmetric ones.