Introduction
The stabilization of bone parts during surgical fracture treatment plays a crucial role in the bone healing process. Research shows that applying small mechanical loads can enhance tissue regeneration, whereas excessive loading can disrupt it. In addition, factors such as the patient's anatomy, activity level, and fracture geometry directly influence the mechanical conditions at the bone fracture site. As a result, a well-controlled mechanical loading of the bone fracture is the primary driver of the healing process. However, local interfragmentary kinematics remain unknown in human patients, with no direct investigation or measurements performed to date.
Project goals
By investigating the mechanical conditions at bone fracture sites, we aim to assess the local interfragmentary motion occurring in human patients and differentiate between favorable and negative factors of influence. This will allow us to confirm the validity of studies performed on large animals and compare the resulting tissue deformations to numerical simulations. Furthermore, we want to correlate various fracture shapes with the healing outcome through statistical analysis of a large database of fracture cases. This project will also lay the groundwork for recommendations on human fracture fixation (e.g., plate working length, plate position, screw positioning), as well as pave the way for personalized fracture treatment.
Strain analysis in the fracture gap
Animal experiments have shown that a certain level of compression at the bone fracture site can improve healing, while shear movement delays it. However, there is currently no data available to verify if the findings derived from large animals are also valid for humans. Furthermore, it is also largely unknown how the shape and positioning of a bone fixation plate (osteosynthesis) influence the local mechanical conditions at the fracture site. Only recently has gait analysis combined with in silico musculoskeletal modeling been able to predict patient-specific interfragmentary loads. Despite the existence of such data for a small number of total joint replacement patients, a large group of human fracture patients have yet to undergo in vivo measurements of the interfragmentary motion.
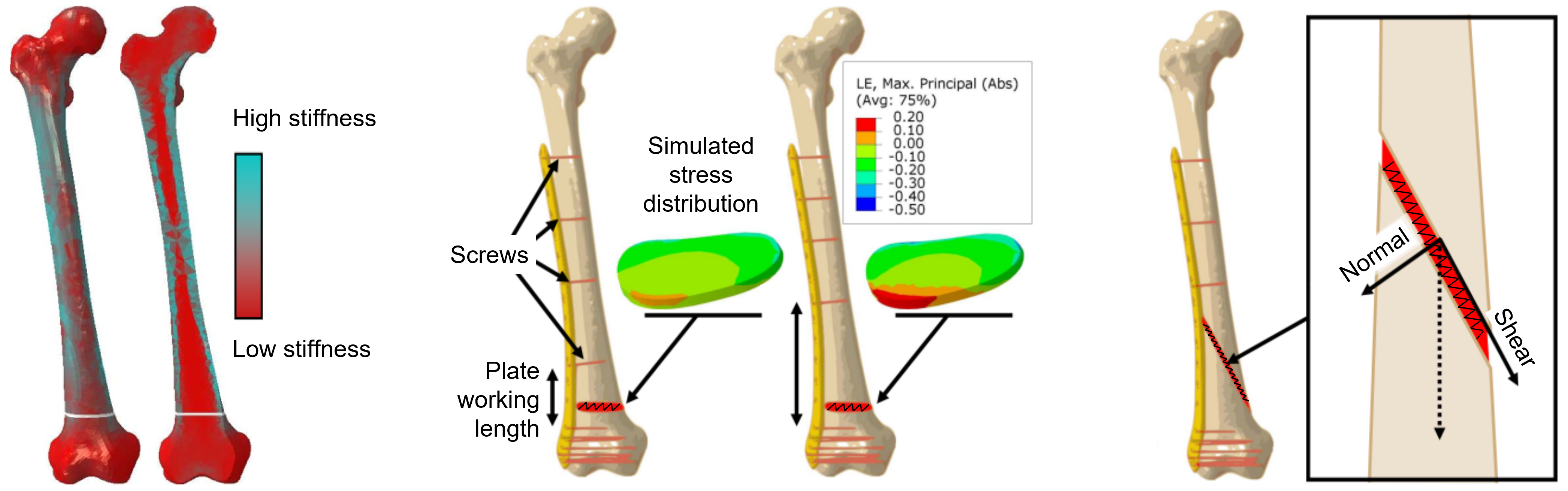
Fig. 1. In silico experiments of the fracture gap. Simulations with the finite element method (FEM) show that varying bone density, screw placement, and fracture angle influence the stress distribution and stress type (compression vs. shear) within the fracture gap even when the same fixation plate is used.
Measuring interfragmentary Motion
In order to measure the patient-specific interfragmentary motion, a special bi-planar video fluoroscopy imaging system has been developed and set up at the OrthoLoad Lab, which is operated by our project partners from Charité University Medicine Berlin and Julius Wolff Institute (JWI). Bi-planar fluoroscopy consists of two pairs of X-ray emitters and receivers that are positioned on movable robotic arms. This enables us to simultaneously monitor the fracture gap from two different perspectives in real-time under normal loading conditions while the patient is standing or walking on a treadmill. However, since the analysis of patient-specific interfragmentary motion is inherently a three-dimensional (3D) problem and bi-planar fluoroscopy is only capable of acquiring two-dimensional (2D) X-ray image data, we have to employ a specialized reconstruction algorithm, known as a 2D-3D registration, in order to measure the actual 3D kinematics.

Fig. 2. Bi-planar video fluoroscopy setup with a radio-opaque bone phantom during the initial imaging tests.

Fig. 3. Imaging test of a cadaver knee bone. The obtained bi-planar X-ray images have high resolution and excellent quality but a limited field of view.
Automated 2D-3D registration
The 2D-3D registration is generally capable of reconstructing patient-specific fracture geometry from only one or two planar X-ray images. Similar methods have already been employed at ZIB in the past in multiple studies and have demonstrated that 3D reconstruction of knee joint kinematics and implant position is possible. The existing registration methods will now be extended to movements of tibia and femur bone fragments and fracture gaps under realistic loading conditions. For more information about 2D-3D registration algorithms, please look at related projects on 3D Reconstruction of Anatomical Structures from 2D X-ray Images and Dynamic Multi-model Knee Joint Registration.
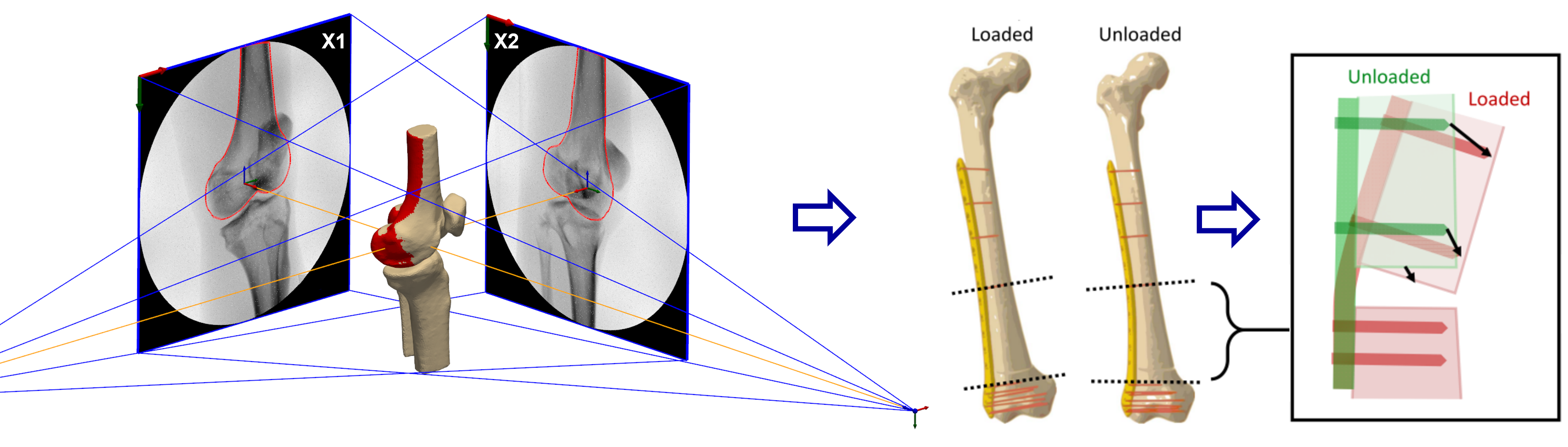
Fig. 4. Virtual bi-planar fluoroscopy setup for an in silico example of 2D-3D registration of a proximal femur bone. The registration solution (red) almost perfectly matches the reference solution (brown). Relative motion between rigid bone segments will be used to estimate the stress and strain distributions within the fracture gap.
The aforementioned intensity-based 2D-3D registration methods are generally limited by the use of local optimization methods, which cause the registration to result in false image-model alignments if not provided with a good enough initial guess on the bone’s position and orientation. This limits the use of 2D-3D registration, as the process of creating the initial guess involves manual positioning, which is especially time-consuming considering we have to process a large number of different patients and imaging experiments. To avoid this issue, we tested various global optimization methods, such as differential evolution (DE) or evolutionary strategy (ES). Such methods can sample a large number of possible solutions, removing the need for tedious manual positioning, increasing registration accuracy, and increasing the automation level of 2D-3D registration.
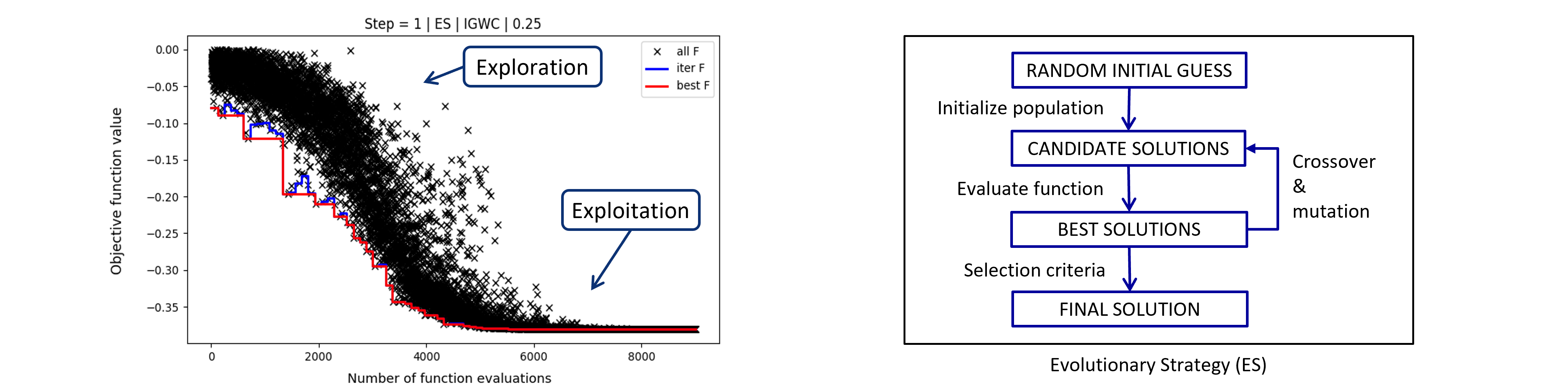
Fig. 5. Optimization convergence plot of 2D-3D registration with evolutionary strategy (ES). ES is a metaheuristic global optimization method inspired by biological evolution. The global optimization method first searches for the most promising solutions, which it then refined in later optimization stages (exploration vs. exploitation).
Validation study
Sub-millimeter precision of 2D-3D registration of bi-planar X-ray images is needed in order to evaluate small movements in the fracture gap. Thus, a validation study was performed before experiments with real patients could begin. For the validation study, an artificial femur bone was cut in two pieces and stabilized with a real fixation plate in order to mimic the fracture gap. The bone was then fitted with optical markers and placed inside a custom-built compression testing machine, which is able to mimic real-world bone loading scenarios. As the bone was dynamically loaded during the X-ray imaging session, the positions of the optical markers were recorded with a PONTOS M5 optical system that has a reported average accuracy of 5.3 micrometers.

Fig. 6. Validation study using a phantom femur bone fitted with a real fixation plate and PONTOS optical markers. Fixation plate and screws are clearly visible on the obtained X-ray image of the bone during compressive loading.
Statistical analysis of fracture cases
Together with our project partners at the JWI, we conducted a retrospective study of a total of 187 tibial and femoral fracture cases between 2005 and 2022. Here, we performed a statistical analysis of the modified Radiographic Union Score for Tibial Fractures (mRUST) at different time points after the initial bone fracture in relation to various patient-specific factors such as age, weight, implant type, and fracture type. The mRUST score evaluates cortical bridging at four landmarks of the fractured bone and is correlated with the biomechanical strength of the fracture site. The results of the analysis show an average healing rate of 0.334 mRUST per week, which leads to an average recovery time of around 8 months for femur and tibia bones.
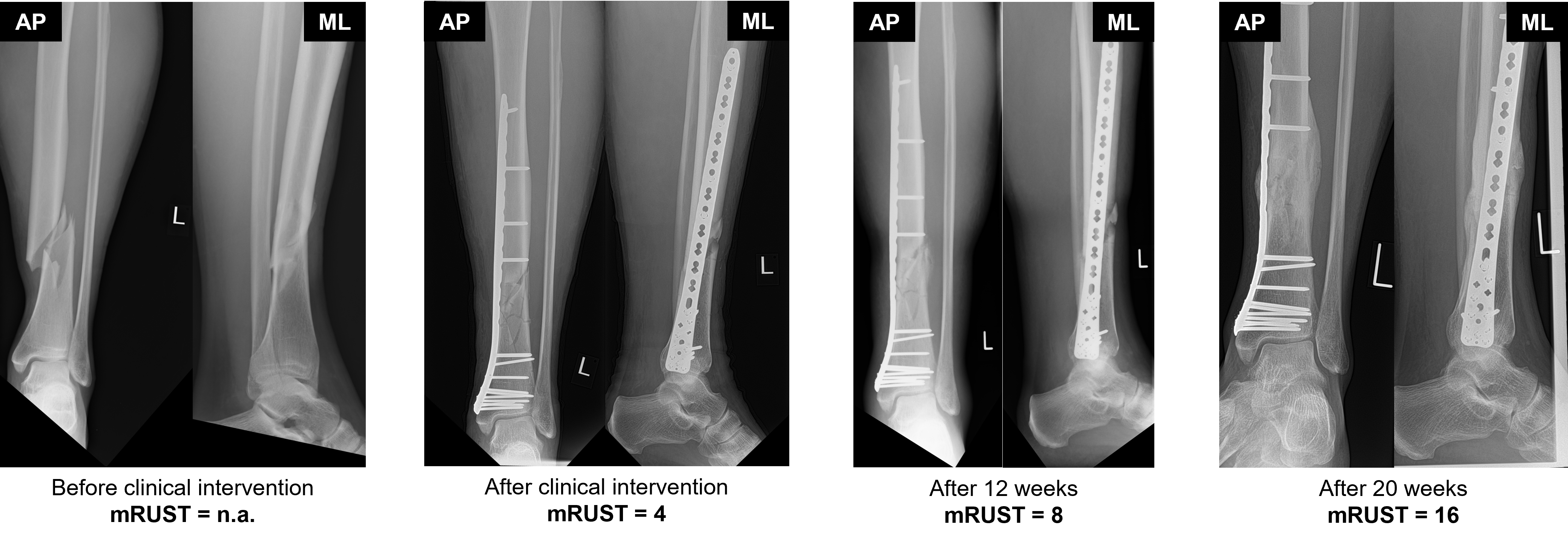
Fig. 7. Evaluation of the mRUST score for femur shaft fracture at four time points following the clinical intervention. The mRUST score requires two perpendicular radiographs of the fracture size that are typically taken from anterior-posterior (AP) and medio-lateral (ML) views.
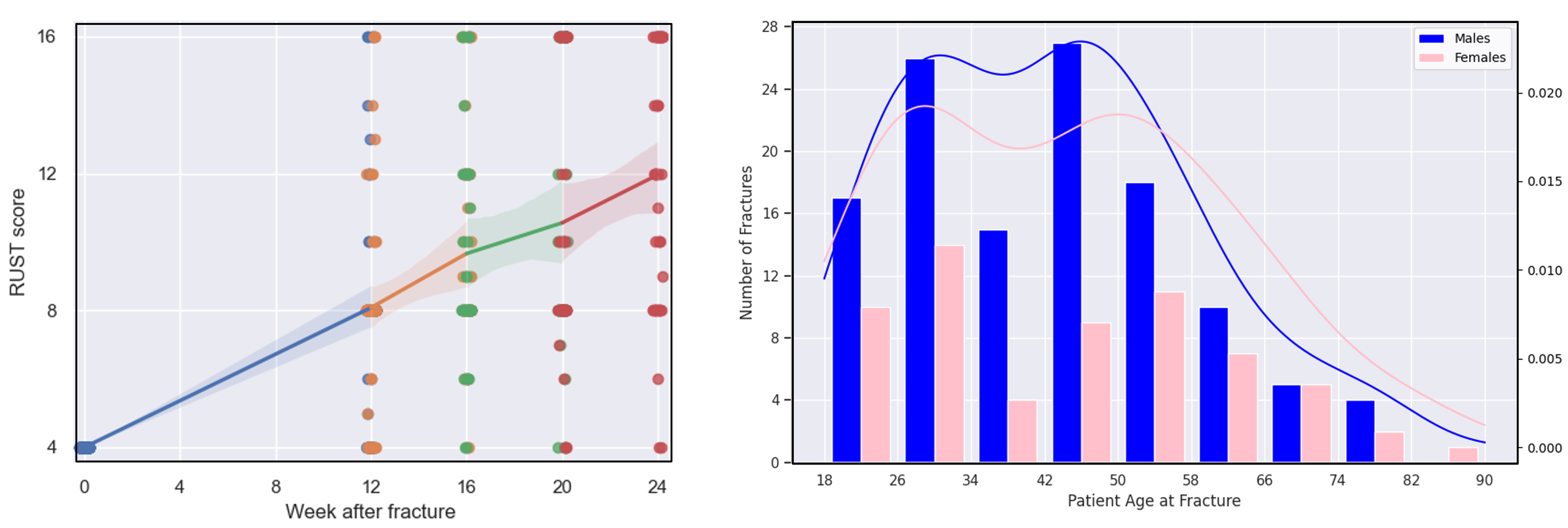
Fig. 8. Average increase of the mRUST score (left) and the distribution of analyzed fracture cases according to demographics (right).