This research is carried out in the framework of MATHEON supported by Einstein Foundation Berlin.
Introduction
In biotechnology, systems biology, or chemical engineering one is faced with large systems of ordinary di erential equations (ODEs) that are used to describe the kinetics of the reaction network of interest. These models contain a large number of unknown parameters that one needs to infer from experimental data. The associated parameter identi cation problem is an inverse problem where knowledge about the uncertainty of the estimated parameters is of utmost importance, e.g., for designing further experiments. Classical parameter identification lacks possibilities to quantify such uncertainties and in addition faces the problem of non-identifiable parameters, especially in realistic biological models. Therefore, Bayesian approaches, that have become realizable due to higher compuational power of modern computers, have experienced a huge revival in the 21st century. A huge disadvantage of these methods, however, is the requirement of prior knowledge about the distribution of the parameters, which has lead to a lot of critique concerning the objectivity Bayesian inference.
| Classical estimators (ML, Gauß-Newton) | Bayesian Inference |
+ are computationally inexpensive, - usually cannot identify all parameters, - lack possibilities to quantify uncertainty, - can result in ill-posed problems, - do not incorporate prior knowledge about parameters.
| - is computationally more expensive + provides distribution of all parameters + can quantify uncertainty + provides well-posed problems [Stuart 2010] + incorporates prior knowledge - requires prior knowledge even when it’s not accessible. |
Fortunatally, there are other methods, called empirical Bayes methods, that can tackle this problem by recovering the prior distribution from the data in certain cases, namely, if the data contains measurements for several individuals (patients). Note, that in such a case the upper two approaches would treat each patient separately when computing patient-specific parametrizations, making no use of the fact that data is given for several patients. Empirical Bayes methods incorporate the data of all patients to first estimate the prior distribution of the parameters and then use standard Bayesien inference for patient-specific parameter estimation.
We aim at implementing such methods for large system-biological models such as the human menstrual cycle. Our work flow has the following stucture:
(1) Compute the likelihood functions from the data of each patient.
(2) Construct a prior distribution as described by the algorithm below.
(3) Use Bayesian inference to compute the posteriors for each patient from the prior and the individual likelihoods.
(4) Make patient-specific predictions, e.g. success rates of certain treatments.
Algorithm for the Prior Estimation
The estimation of the prior is realized via an iterative algorithm. Starting with a "wide, non-informative" prior p0 we repeat the following steps for n=0,1,...:
(1) Compute the posterior distribution for each patient (standard Bayesian inference) with respect to the current prior pn.
(2) Choose the updated prior pn+1 as the (pointwise) mean of these posteriors.
This algorithm can be proven to maximize the marginal likelihood. However, for a finite amount of data it starts peaking at certain parametrizations, which can also be shown theoretically. We are currently working on getting rid of these peaks by regularisation techniques.
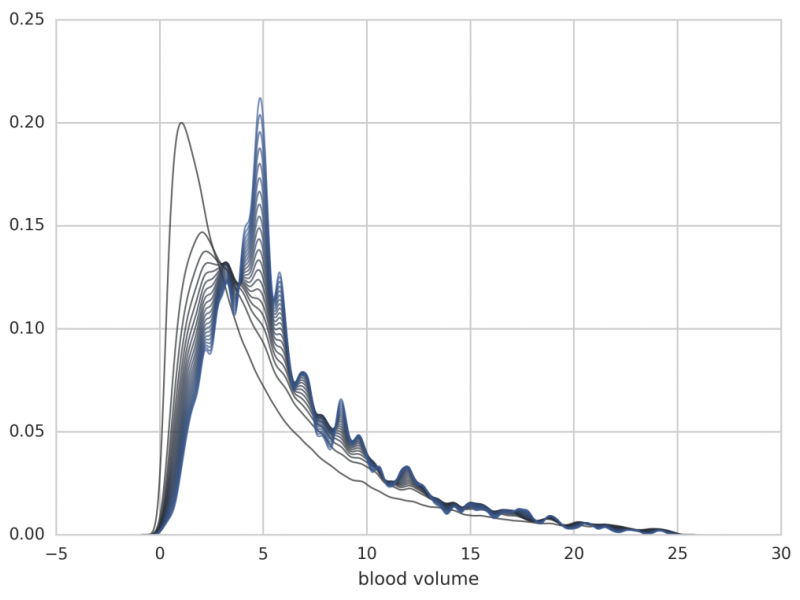
The application to the human menstrual cycle (modeled by a 33-dimensional ODE with 114 unknown parameters) is shows below. Note, that the algorithm is applied in the high-dimensional parameter space and the results show the distribution of only one parameter, all others being integrated out.
Figure: First iteration step from p0 (uniformly distributed) to p1 (in blue). p1 is chosen as the mean of the patients' individual posteriors (thin lines).
Figure: Further iterations from p1 to p20 (the individual posteriors are no longer plotted). Note that the distribution is shifted towards a blood volume of 5 liters, which is a typical value for adults.