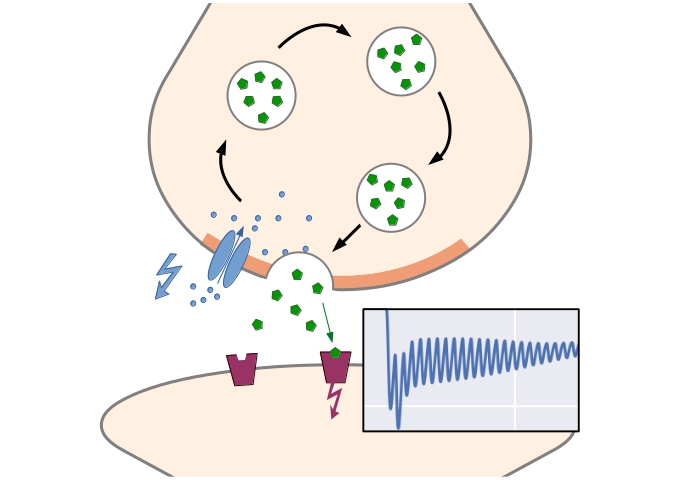
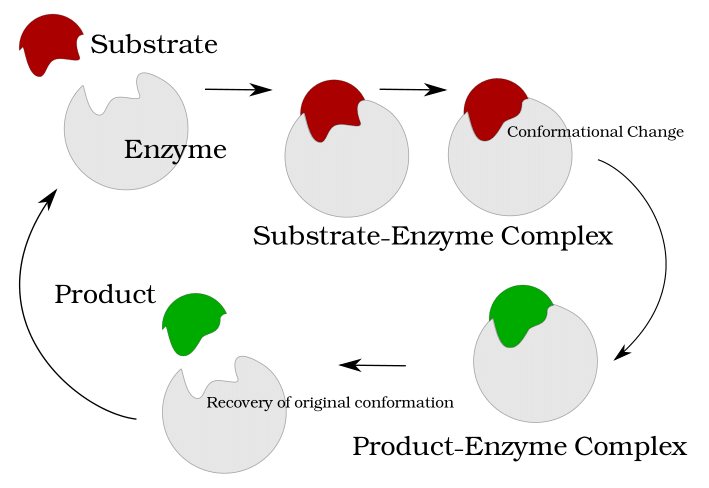
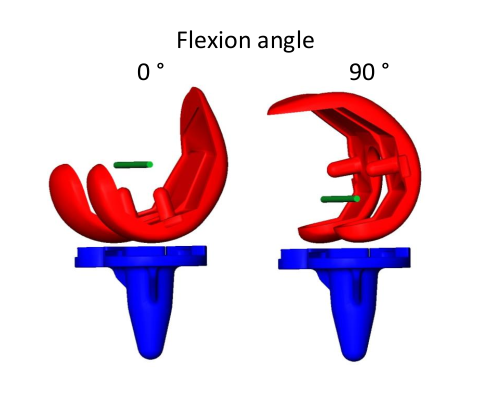
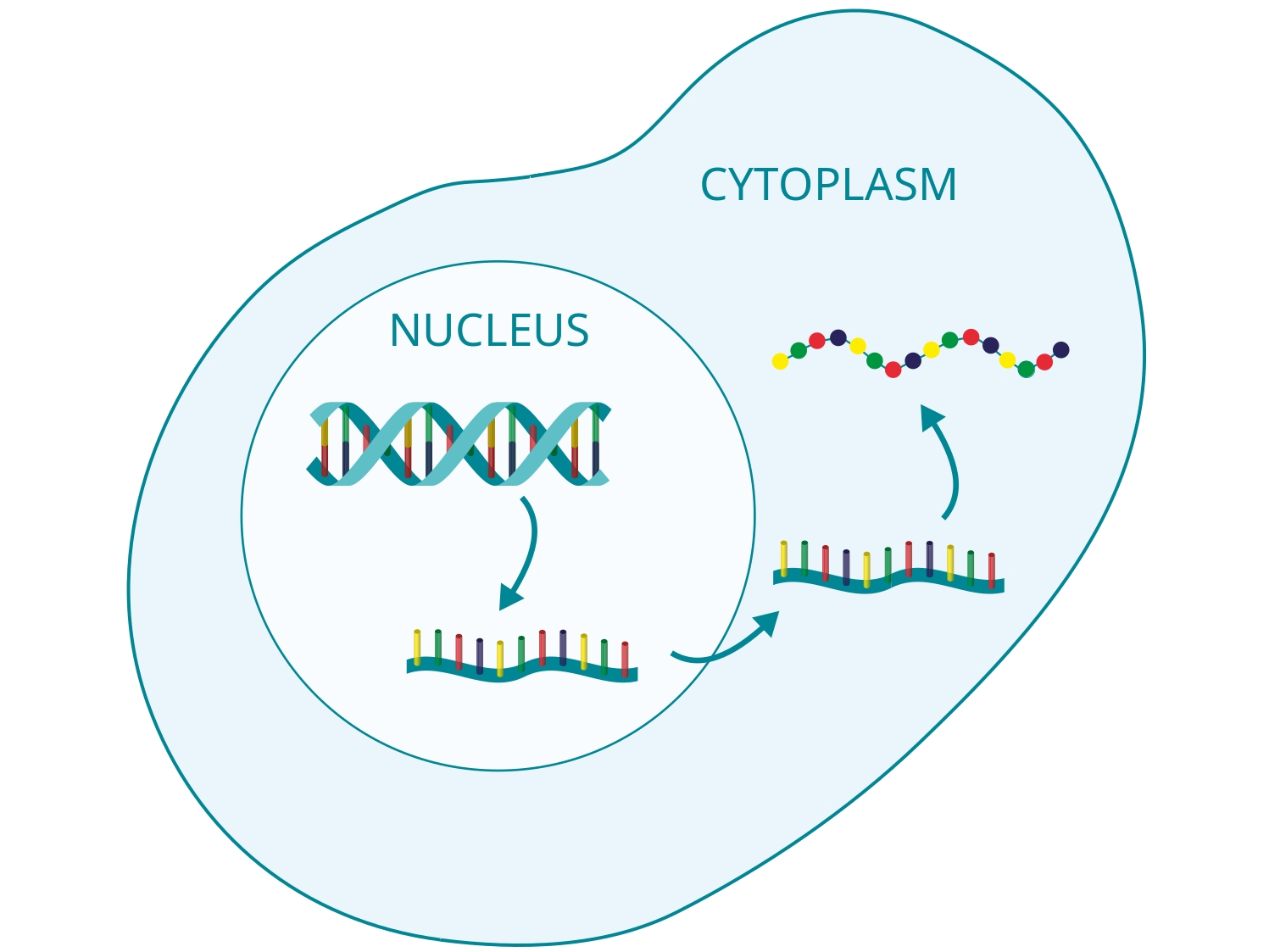
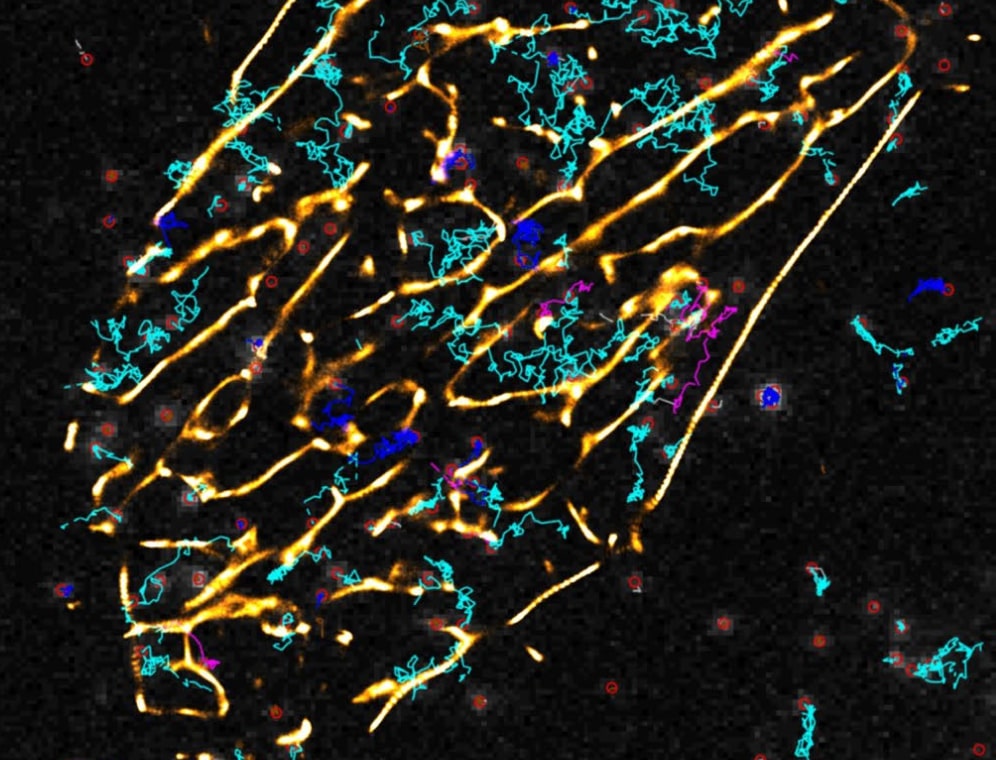
Computational Systems Biology aims at the construction and analysis of predictive mathematical models for the description of complex interactions in biological and biochemical systems. Modelling approaches range from stochastic microscopic description which follow the spatial movement and biochemical interactions of individual particles, over spatially well-mixed kinetics given by Markov jump processes, to deterministic systems given by ordinary differential equations (ODEs), that describe the concentrations of substances over time, or partial differential equations for spatially resolved dynamics.
Motivated by the multi-scale nature of biological systems, we consider hybrid models that combine the different mathematical formalisms, e.g. ODEs for metabolic networks with discrete dynamical systems for regulatory processes, or spatially well-mixed kinetics connected by rare diffusive jumps between cellular subdomains. Efficient numerical algorithms and computational techniques are developed and applied in order to study the dynamical systems. Applications range from cellular signalling pathways to physiological processes on a whole-organism level, for example endocrinological networks, and also include classical reaction kinetics.
Our work is highly interdisciplinary. Therefore we are actively establishing academic and industrial collaborations with different partners to validate and to improve our models.
Topics of interest
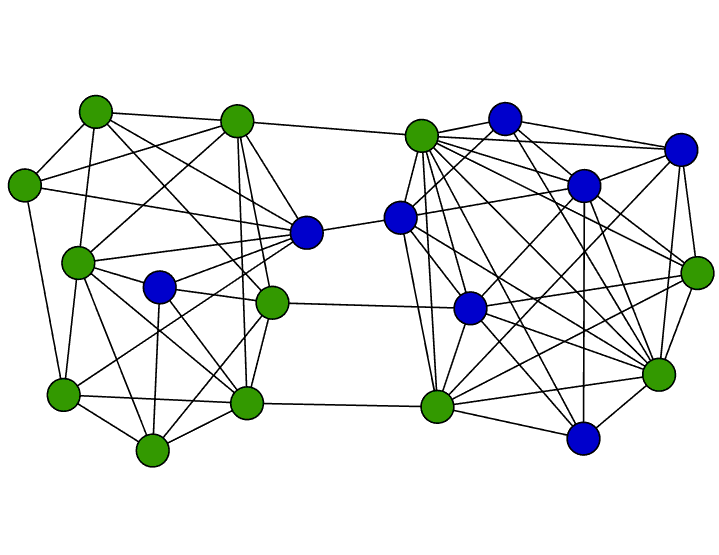
Concentration effects for stochastic dynamics on networks of interacting agents